最適化問題(optimization problem) - kanetaiの二次記憶装置

基本的に連続でn回微分可能を仮定しておく。

$\max.$	$f(x)$	目的関数(objective function)
s.t.	$g(x) \geq 0$	不等式制約(inequality constraint)
	$h(x)=0.$	等式制約(equality constraint)

実行可能解(feasible solution) 制約を満たす解
実行可能領域(feasible region) 実行可能解の集合
解を加減乗除や初等関数の合成関数で表される(閉形式;closed-form)場合、解析に解ける(analytically solvable)問題と言う。

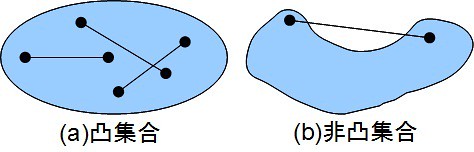
凸集合(convex set)と凸関数(convex function)

$A \subseteq \mathbb{R}^d$ , 任意の ${\bf x}^{(1)} \in A, {\bf x}^{(2)} \in A$ , 任意の $t\in [0,1]$ があったとき、
$t{\bf x}^{(1)}+(1-t){\bf x}^{(2)} \in A$ $\Rightarrow$ $A$ は凸集合(convex set)
※ $t\in [0,1]$ のとき $t{\bf x}^{(1)}+(1-t){\bf x}^{(2)}$ は ${\bf x}^{(1)},{\bf x}^{(2)}$ を結ぶ直線を表していることに注意する(線分のベクトル方程式).

平面 $\{ {\bf x}|{\bf m}^T {\bf x} + b = 0, {\bf x}\in \mathbb{R}^d \}$ , 半空間 $\{{\bf x}|{\bf m}^T {\bf x} + b \geq 0, {\bf x}\in \mathbb{R}^d \}$
は凸集合

A,Bが凸集合	$\Rightarrow$	$A \cap B$ も凸集合
		※ $A \cup B$ は凸集合になるとは限らない

( 言語処理のための機械学習入門 (自然言語処理シリーズ) p7)

上にと凸な関数を凹関数(concave function)、下にと凸な関数を凸関数(convex function)という。
※スカラー値関数に対してのみ定義されるもの
※上下が逆なだけで、持つ性質は共通しているので、二つまとめて凸関数と表現することもある。
任意の ${\bf x}^{(1)}, {\bf x}^{(2)} \in \mathbb{R}^d$ 、任意の $t\in [ 0,1]$ に対し、
$f(t{\bf x}^{(1)}+(1-t){\bf x}^{(2)}) \geq tf({\bf x}^{(1)}) + (1-t)f({\bf x}^{(2)}) \Rightarrow f({\bf x})$ は上に凸
$f(t{\bf x}^{(1)}+(1-t){\bf x}^{(2)}) \leq tf({\bf x}^{(1)}) + (1-t)f({\bf x}^{(2)}) \Rightarrow f({\bf x})$ は下に凸

上に凸関数の和は上に凸な関数

$f({\bf x})$ が上に凸な関数、 $a$ が非負の定数 $\Rightarrow$ $af({\bf x})$ も上に凸

(言語処理のための機械学習入門 (自然言語処理シリーズ)p8)

凸関数であるための1次の条件}(first-order convexity condition)

任意の ${\bf x}^{(1)}\in \mathbb{R}^d$ , ${\bf x}^{(2)}\in \mathbb{R}^d$ について、
関数 $f$ は上に凸 $\Leftrightarrow f({\bf x}^{(2)}) - f({\bf x}^{(1)}) \leq (\nabla f({\bf x})|_{{\bf x}={\bf x}^{(1)}})^T ({\bf x}^{(2)} - {\bf x}^{(1)})$
関数 $f$ は下に凸 $\Leftrightarrow f({\bf x}^{(2)}) - f({\bf x}^{(1)}) \geq (\nabla f({\bf x})|_{{\bf x}={\bf x}^{(1)}})^T ({\bf x}^{(2)} - {\bf x}^{(1)})$
(言語処理のための機械学習入門 (自然言語処理シリーズ)p9では $d=1$ )
(http://infoshako.sk.tsukuba.ac.jp/~yoshise/Course/DC/cvx-handout.pdf)
※上に凸関数は全ての接線がその関数の上側にくることを示している。
※スカラー値関数： $f({\bf x})$ , 変数： ${\bf x} = [ x_1, x_2, \cdots , x_d$ ^T ]に対して
ハミルトン演算子(Hamiltonian)： $\nabla = \left [ \frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \cdots , \frac{\partial}{\partial x_d} \right ] ^T$
勾配(gradient)： $\nabla f({\bf x}) = \mathrm{grad} f({\bf x}) = \frac{\partial f({\bf x})}{\partial {\bf x}} = \left [ \frac{\partial f({\bf x})}{\partial x_1}, \frac{\partial f({\bf x})}{\partial x_2} , \cdots , \frac{\partial f({\bf x})}{\partial x_d} \right ] ^T$

凸関数であるための2次の条件(second-order convexity condition)

1変数の場合
1変数関数 $f$ は上に凸 $\Leftrightarrow$ 2階微分 $f"(x)$ は常に負
1変数関数 $f$ は下に凸 $\Leftrightarrow$ 2階微分 $f"(x)$ は常に正
多変数の場合
多変数関数fは上に凸 $\Leftrightarrow {\bf H}(f({\bf x}))$ は半負定値
多変数関数fは下に凸 $\Leftrightarrow {\bf H}(f({\bf x}))$ は半正定値
※スカラー値関数： $f({\bf x})$ , 変数： ${\bf x} = [ x_1, x_2, \cdots , x_d ]^T$ に対して
ヘッセ行列(Hessian matrix)：
${\bf H}(f({\bf x})) = \nabla \nabla ^ T f({\bf x})= \left[ \begin{array}{cccc} \frac{\partial ^2 f({\bf x})}{\partial x_1 ^2}& \frac{\partial ^2 f({\bf x})}{\partial x_1 \partial x_2} & \cdots & \frac{\partial ^2 f({\bf x})}{\partial x_1 \partial x_d} \\ \frac{\partial ^2 f({\bf x})}{\partial x_1 \partial x_2} & \frac{\partial ^2 f({\bf x})}{\partial x_2 ^2} & \cdots & \frac{\partial ^2 f({\bf x})}{\partial x_2 \partial x_d} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial ^2 f({\bf x})}{\partial x_d \partial x_1} & \frac{\partial ^2 f({\bf x})}{\partial x_d \partial x_2} & \cdots & \frac{\partial ^2 f({\bf x})}{\partial x_d ^2} \end{array} \right ]$
※任意の ${\bf x}$ に対して、2次形式 ${\bf x}^T {\bf A} {\bf x} > 0 \Leftrightarrow {\bf A}$ は正定値行列(positive definition matrix)または、正定値(正の定符号)(positive definite)であるという。
$=0$ を含む場合は半正定値(positive semi-definite), 不等号が逆の場合はそれぞれ、負定値(negative definite)、半負定値(negative semi-definite)という。
(言語処理のための機械学習入門 (自然言語処理シリーズ)p11)

凸計画問題(convex programming problem)

凸計画問題：目的関数が凸関数で、実行可能領域が凸集合である最適化問題( 改善する方向に進んでいけば解にたどり着く)
$A,B$ が凸集合のとき、 $A\cup B$ は凸集合とは限らないが、 $A$ での最適解と $B$ での最適解の良いほうが $A\cup B$ の最適解になる(言語処理のための機械学習入門 (自然言語処理シリーズ)p12)

数値的解法(numerical method)(言語処理のための機械学習入門 (自然言語処理シリーズ)p13)
・際急勾配法(gradient method)：目的関数の傾きが最も急な方向に変数の値を変化させていく。
${\bf x}^{new} = {\bf x}^{old} + \epsilon \nabla f({\bf x})|_{{\bf x}={\bf x}^{old}}$
最大化が目的：目的関数が最も増加する方向に進む最急上昇法(gradient ascent method)( $\epsilon > 0$ )、
最小化が目的：目的関数が最も減少する方向に進む最急降下法(gradient descent method)( $\epsilon < 0$ )
・ニュートン法(Newton's method)
証明は2次までのテイラー展開したものを $\Delta x_i$ で偏微分=0とおいてほげほげ(これなら分かる最適化数学―基礎原理から計算手法までpp.88-89).
収束は速いが、逆行列の計算が高価なので、高速近似手法を用いることが多い。
${\bf x}^{new} = {\bf x}^{old} + \epsilon [ {\bf H}(f({\bf x}))^{-1} \nabla f({\bf x}) ]_{{\bf x}={\bf x}^{old}}$
最大化が目的： $\epsilon > 0$
最小化が目的： $\epsilon < 0$
$\epsilon$ は学習率で定数である。ただし、直線探索を行う場合は定数ではない(2分探索など)。

Newton・Raphson法はもともと、(連立)非線形方程式 ${\bf f}({\bf x})=0$ を解く方法
(C言語による数値計算入門―解法・アルゴリズム・プログラム (UNIX & Information Science) pp.86-88)
${\bf x}^{new} = {\bf x}^{old} - \epsilon [ {\bf J}({\bf f}({\bf x}))^{-1} {\bf f}({\bf x}) ]_{{\bf x} = {\bf x}^{old}}$
※ベクトル値関数： ${\bf f}({\bf x}) = [ f_1({\bf x}), f_2({\bf x}), \cdots , f_d({\bf x})]^T$ , 変数： ${\bf x} = [ x_1, x_2, \cdots , x_d ]^T$ に対して、
ヤコビ行列(Jacobian matrix)：
${\bf J}({\bf f}({\bf x})) = {\bf f}({\bf x}) \nabla ^T = \left [ \begin{array}{cccc} \frac{\partial f_1({\bf x})}{\partial x_1} & \frac{\partial f_1({\bf x})}{\partial x_2} & \cdots & \frac{\partial f_1({\bf x})}{\partial x_d} \\ \frac{\partial f_2({\bf x})}{\partial x_1} & \frac{\partial f_2({\bf x})}{\partial x_2} & \cdots & \frac{\partial f_2({\bf x})}{\partial x_d} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_d({\bf x})}{\partial x_1} & \frac{\partial f_d({\bf x})}{\partial x_2} & \cdots & \frac{\partial f_d({\bf x})}{\partial x_d} \\ \end{array} \right ]$

等式制約付凸計画問題

ラグランジュの未定乗数法}(the method of Lagrange multipliers)

ラグランジュ関数を偏微分して0とおいたものと、束縛条件の連立方程式を解く
ラグランジュ関数(Lagrangian)： $L({\bf x},{\bf \lambda}) = f({\bf x}) + {\bf \lambda}^T {\bf g}({\bf x})$
ラグランジュ乗数(Lagrange multiplier)(のベクトル)： ${\bf \lambda} = [ \lambda _1 , \lambda _2 , \cdots , \lambda _k ] ^T$ ( $k$ は制約の数)
$\begin{array}{cc} \max. & f({\bf x}) \\ s.t. & {\bf g}({\bf x}) = {\bf 0} \end{array}$
最適解はラグランジュ乗数法より
${ \begin{cases} \nabla f({\bf x}) + \nabla( {\bf \lambda}^T{\bf g}({\bf x}) ) = {\bf 0} \\ {\bf g}({\bf x}) = {\bf 0} \end{cases} }$
の解となる。
※ラグランジュ乗数法は条件付極値問題を解く手法。したがって、凸性が成立している必要がある。

不等式制約付き凸計画問題}

$\begin{array}{cc} \max. & f({\bf x}) \\ s.t. & {\bf g}({\bf x}) \geq {\bf 0} \end{array}$
ラグランジュ関数(Lagrangian)： $L({\bf x},{\bf \lambda}) = f({\bf x}) + {\bf \lambda}^T {\bf g}({\bf x})$
ただし、 ${\bf \lambda} = [ \lambda _1 , \lambda _2 , \cdots , \lambda _k ] ^T \geq {\bf 0}$ とする。
凸計画問題では鞍点が最適解となる。
鞍点(saddle point)： $L({\bf x},{\bf \lambda}^* ) \leq L({\bf x}^* ,{\bf \lambda}^* ) \leq L({\bf x}^* ,{\bf \lambda})$ を満たす点 $\left [ \begin{array}{c} {\bf x}^* \\ {\bf \lambda}^* \end{array} \right ]$
したがって、まず $L({\bf x},{\bf \lambda})$ を ${\bf x}$ について最大化し(主問題;primal problem)、そのうえで $L({\bf x}({\bf \lambda}),{\bf \lambda})$ を ${\bf \lambda}$ について最小化(双対問題;dual problem)すれば良い。 ${\bf x}^*$ が閉形式にならない場合は、 ${\bf x}$ の更新と、 ${\bf \lambda}$ の更新を交互にするなどの工夫が必要。
双対問題の制約は ${\bf \lambda} = [ \lambda _1 , \lambda _2 , \cdots , \lambda _k ] ^T \geq {\bf 0}$ だけなので扱いやすい。