A Figure on Surface(AOJ No.0036), Path on a Grid(AOJ No.0037), Poker Hand(AOJ No.0038), Roman Figure(AOJ No.0039), Affine Cipher(AOJ No. 0040)

リポジトリ

A Figure on Surface(AOJ No.0036)

8×8の0,1パターンが与えられる。
その中で、
A
■■
■■
B
■
■
■
■
C
■■■■
D
　■
■■
■
E
■■
　■■
F
■
■■
　■
G
　■■
■■
のどれかのパターンが1つだけ埋め込まれている(■->1, otherwise->0)
与えられるパターンにはA〜G以外のパターンが埋め込まれていることはない。
埋め込まれているパターンはA〜Gのどれか。

コード

import java.util.*;
public class aoj0036 {
	static final Scanner stdin = new Scanner(System.in);
	static boolean[][] map = new boolean[11][11];
	public static void main(String[] args) {
		while(stdin.hasNext()){
			for(boolean[] r : map) Arrays.fill(r, false);
			int sx = -1, sy = -1;
			for(int i=0; i<8; ++i){
				String l = stdin.next();
				for(int j=0; j<8; ++j){
					if(l.charAt(j) == '1'){
						map[i][j] = true;
						if( sx < 0 ){ sx=j; sy=i;  }
					}
				}
			}
			System.out.println( solve(sx, sy) );
		}
	}
	static String solve(int sx, int sy){
		if( map[sy][sx+1] ){
			if( map[sy][sx+2] ) return "C";
			if( map[sy+1][sx+2] ) return "E";
			if( map[sy+1][sx+1] ) return "A";
			return "G";
		}
		if(map[sy+1][sx+1]) return "F";
		if(map[sy+2][sx]) return "B";
		return "D";
	}
}

Path on a Grid(AOJ No.0037)

5*5のマップが下図のように与えられる(黒線が壁)。
左上が初期位置で、右を向いている。
右手法で進んで行って、初期位置に戻ってくるまでの移動経路(↑U, →R, ↓D, ←Lの系列)を求める。
ただし、点 A から右に 1 区画分は必ず壁がある(入力の最初は必ず1)。

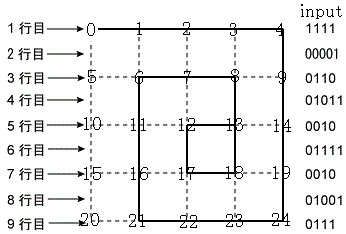
アルゴリズム

入力がややこしいので、上図のように、ノード番号を振って、壁をエッジとして、隣接行列を作る。
そして、初期位置から進行方向に対して、左、前、右、後の優先順位で、壁を移動するすると、右手法で進んだ時と同じ順番で進める(突き当りがあったとき、左に行くと右手が壁になる)。
これを初期位置に戻るまで繰り返す。

縦横を2倍に伸ばして、2ますずつ進むやり方もありかな.

コード

import java.util.*;
public class aoj0037 {
	static final Scanner stdin = new Scanner(System.in);
	//→↑←↓
	static int D = 4; // 4 directions
	static int dx[] = {1, 0,  -1, 0};
	static int dy[] = {0, -1, 0,  1};
	static char out[] = {'R', 'U', 'L', 'D'};
	static int WIDTH = 5;
	public static void main(String[] args) {
		boolean[][] g = new boolean[25][25]; //adjacency matrix
		String str;
		for(int i=0; i<4; ++i){
			str = stdin.nextLine();
			for(int j=0; j<WIDTH-1; ++j)
				if( str.charAt(j) == '1' )
					g[yx2pos(i,j)][yx2pos(i,j)+1] = g[yx2pos(i,j)+1][yx2pos(i,j)] = true;
			str = stdin.nextLine();
			for(int j=0; j<WIDTH; ++j)
				if( str.charAt(j) == '1' )
					g[yx2pos(i,j)][yx2pos(i,j)+WIDTH] = g[yx2pos(i,j)+WIDTH][yx2pos(i,j)] = true;
		}
		str = stdin.nextLine();
		for(int j=0; j<WIDTH-1; ++j)
			if( str.charAt(j) == '1' )
				g[yx2pos(WIDTH-1,j)][yx2pos(WIDTH-1,j)+1] = g[yx2pos(WIDTH-1,j)+1][yx2pos(WIDTH-1,j)] = true;
		System.out.println( solve(g) );
	}
	static int yx2pos(int y, int x){ return WIDTH*y + x;}
	//current coord(y,x), next direction of movement(nd), adjacency matrix(g)
	static boolean check(int y, int x, int nd, boolean[][] g){
		int ny = y + dy[nd], nx = x + dx[nd];
		return ny>=0 && ny < WIDTH && nx>=0 && nx < WIDTH && g[yx2pos(y,x)][yx2pos(ny,nx)];
	}
	static String solve(boolean[][] g){
		int x = 0, y = 0; //current coord
		int d = 0; //current direction of movement →
		StringBuilder res = new StringBuilder();
		do{
			if( check(y, x, (d+1)%D, g) ){ //d + ←
				d = (d+1)%D;
			}else if( check(y, x, d, g) ){ //d + ↑
				;
			}else if( check(y, x, (d+3)%D, g)){ //d + →
				d = (d+3)%D;
			}else{ //d　+ ↓
				d = (d+2)%D;
			}
			x += dx[d]; y += dy[d]; res.append(out[d]);
		}while( !(x==0 && y==0) );
		return res.toString();
	}
}

Poker Hand(AOJ No.0038)

絵柄のない5枚のトランプが与えられたときの、ポーカーの役を求める。
※1を含むストレートは1,2,3,4,5 または、10,11,12, 13, 1

コード

頻度表の最後に1の頻度を加えたものを文字列化し、"11111"をサーチすることでストレートの判定を行った。

import java.util.*;
public class aoj0038 {
	static final Scanner stdin = new Scanner(System.in);
	static Integer[] count = new Integer[13];
	public static void main(String[] args) {
		int[] deal = new int[5];
		while(stdin.hasNext()){
			String[] str = stdin.nextLine().split(",");
			for(int i=0; i<5; ++i) deal[i] = Integer.parseInt(str[i]);
			System.out.println( solve(deal) );
		}
	}
	static String solve(int[] deal){
		Arrays.fill(count, 0);
		for(int n: deal) count[n-1]++;
		StringBuilder str = new StringBuilder("");
		for(int c: count) str.append(""+c);
		str.append( str.charAt(0) );
		Arrays.sort(count);
		switch(count[12]){
		case 4: return "four card";
		case 3: return count[11] == 2 ? "full house" : "three card";
		case 2: return count[11] == 2 ? "two pair" : "one pair";
		case 1: if( str.indexOf("11111") >= 0 ) return "straight";
		}
		return "null";
	}
}

Roman Figure(AOJ No.0039)

I は1, V は5, X は10, L は50, C は100, D は500, M は1000
小さい数が大きい数に続いている、つまり右側にあるときは足す。
小さい数が大きい数の前に、つまり左にあるときは、大きい数から小さい数を引く。
大きい数字の前にあって引き算を表す小さな数字は一回の引き算あたりひとつしかない。←重要
与えられるローマ数字を10進数表記を求める。
(実際のローマ数字ではI はV かX から、X はL かC から、C はD かM からしか引き算しない、また、同じローマ数字は４つ以上（または５つ以上）足し並べることはないが、それらを考慮する必要はない)

コード

HashMapをこういう風に初期化できるんですね

import java.util.*;
public class aoj0039 {
	static final Scanner stdin = new Scanner(System.in);
	@SuppressWarnings("serial") static HashMap<Character, Integer> map = new HashMap<Character, Integer>() {
		{ put('I', 1); put('V', 5); put('X', 10); put('L', 50); put('C', 100); put('D', 500); put('M', 1000); }
	};
	public static void main(String[] args) {
		while(stdin.hasNext()) System.out.println(solve(stdin.nextLine().toCharArray()));
	}
	static int solve(char[] input){
		int res = 0;
		int pre = map.get(input[0]);
		for(char ch: input){
			int cur = map.get(ch);
			res += (pre >= cur ? cur : (cur-pre-pre));
			pre = cur;
		}
		return res;
	}
}

Affine Cipher(AOJ No.0040)

小文字アルファベットとスペースから成る英文が暗号化されて与えられる。
小文字アルファベットをa=0, b=1, ...とし、
(アフィン暗号; Affine Cipher)で暗号化される。
暗号文の原文を求める。
ただし、原文にはthat か thisが含まれており、に対するが一対一対応するように、
が選ばれている(と26は互いに素)。

アルゴリズム

まず、that, thisの全ての暗号化パターンを求めておく。
26で割った剰余で暗号化されているので、(0, 26)の範囲のを使う。
ただし、と26が互いに素、すなわち、になるように、を選ぶ。
次に、4文字の単語とthatとthisの暗号化パターンが一致するときのを探して、復号する。
復号は、
で行う。
※は法26の下での逆元

コード

Javaって、クラスは参照渡しだから、Integerで渡せば、参照になるかと思ったけど、
String クラスと同じように不変クラスで、演算したときに新しいオブジェクトを生成しているのかな?
とりあえず、配列で渡して、参照させたけど、Java面倒すぎる。refキーワードがあったらいいのに。

import java.util.*;
public class aoj0040 {
	static final Scanner stdin = new Scanner(System.in);
	static ArrayList<key> list = new ArrayList<key>();
	static int M = 26;
	public static void main(String[] args) {
		makeList();
		int n = stdin.nextInt(); stdin.nextLine();
		while(n-- >0){
			String[] in = stdin.nextLine().split(" ");
			System.out.println(solve(in));
		}
	}
	static class key{
		int a, b;
		String encoded;
		key(int a, int b, String in){ this.a = a; this.b = b; this.encoded = encode(in, a, b); }
		String encode(String in, int a, int b){
			StringBuilder res = new StringBuilder(in);
			for(int i=0; i<res.length(); ++i)
				res.setCharAt(i, (char)((a*(res.charAt(i)-'a') + b)%M + 'a') );
			return res.toString();
		}
	}
	static void makeList(){
		for(int a=1; a<M; ++a)
			for(int b = 0; b<M; ++b)
				if(isCoprime(a,M) ){
					list.add(new key(a, b, "that")); list.add(new key(a, b, "this"));
				}
	}
	static String decode(String out, int a, int b){
		StringBuilder res = new StringBuilder(out);
		for(int i=0; i<res.length(); ++i)
			res.setCharAt(i, (char)( (res.charAt(i)-'a' - b + M )*modInverse(a,M) % M + 'a' ) );
		return res.toString();
	}
	static String solve(String[] in){
		int a=0, b=0;
		StringBuilder res = new StringBuilder();
		RET: for(String str: in){
			if(str.length() == 4)
				for(key k: list)
					if(k.encoded.equals(str)){
						a = k.a; b = k.b;
						break RET;
					}
		}
		for(int i=0; i<in.length; ++i) res.append(" " + decode(in[i], a, b));
		return res.substring(1);
	}
	public static final int[] swap(int[] x, int i, int j){ int tmp = x[i]; x[i] = x[j]; x[j] = tmp; return x; }
	public static final int GCD(int a, int b){ return b == 0 ? a : GCD(b, a%b); }
	public static int extGCD(int a, int b, int x[]){
		int g = a;
		x[0] = 1; x[1] = 0;
		if (b != 0){
			g = extGCD(b, a % b, x);
			swap(x, 0, 1);
			x[1] -= (a / b) * x[0];
		}
		return g;
	}
	public static int modInverse(int a, int m){
		int[] x = new int[2];
		return (extGCD(a, m, x) == 1) ? (x[0] + m) % m : 0;
	}
	public static boolean isCoprime(int a, int b){ return GCD(a,b) == 1; }
}