平面幾何(交差判定) - kanetaiの二次記憶装置

intersect_LS
intersect_LP

直線

平面幾何(plane geometory)
を使って、直線クラスを作ってみた。(直線(line)といいつつも、線分(segment)としても使うので注意)

public static class Line{
	private final Point start;
	private final Point end;
	public Line(double sx, double sy, double ex, double ey){ start = new Point(sx,sy); end = new Point(ex,ey); }
	public Line(Point start, Point end){ this.start = new Point(start); this.end = new Point(end); }
	public Point dirV() { return end.sub(start); } //directional vector
	public double distance() { return end.distance(start); }
	public void set(double sx, double sy, double ex, double ey){ start.x = sx; start.y = sy; end.x = ex; end.y = ey; }
	public void set(Point start, Point end){ set(start.x, start.y, end.x, end.y); }
	public void set(Line l){ set(l.start, l.end); }
        public final int ccw(Point p){ return start.ccw(end, p); }
//abbr.
} //class Line

直線 $L(\vec{l_s l_e })$ と直線 $M(\vec{m_s m_e })$

$\vec{v}\parallel \vec{u} \Leftrightarrow cross(\vec{v}, \vec{u})=0$ を利用して交差判定できる。
同一直線のものも平行とすると、
$cross(L, M) \neq 0$ または $cross(L, M) = 0$ , $cross(L, \vec{l_e , m_s })= 0$ のとき交差していることがわかる
別に $\vec{l_e, m_s }$ を使わなくても、 $L$ 上のある点と $M$ 上のある点を結ぶベクトルなら多分なんでもおｋ
実装するときは、位置がdoubleなので、EPSを使って判定する。

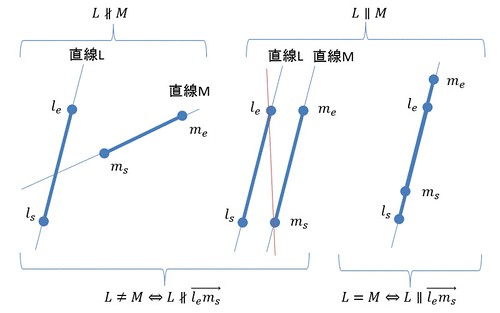
//instance method of Line class
public final boolean intersectsLL(Line m) {
	Point lv = this.dirV(), mv = m.dirV();
	return Math.abs(lv.cross(mv)) > EPS || // non-parallel
		Math.abs(lv.cross(mv.mul(-1))) < EPS;     // same line
}

交点座標は、 $(1-\lambda )\vec{l_s} + \lambda \vec{l_e} = \mu \vec{m_s}+(1-\mu)\vec{m_e}$ $0<\lambda ,\mu < 1$
$\xi = (\vec{m_e}-\vec{l_s})\times (\vec{m_e}-\vec{m_s})$
$\eta = (\vec{l_e}-\vec{l_s})\times (\vec{m_e}-\vec{l_s})$
$\delta = (\vec{l_e}-\vec{l_s})\times (\vec{m_e}-\vec{m_s})$
とすると
$\lambda = \frac{\xi}{\delta}, \mu = \frac{\eta}{\delta}$
左辺を整理した式を使うと交点の座標は $\vec{l_s} + \lambda (\vec{l_e}-\vec{l_s})$
線分の場合は、これに加えて、交差チェックすればいい。

//instance method of Line class
public final Point intersectionLLPoint(Line m){
	Point mp = m.dirV(), lp = this.dirV();
	double A = m.end.sub(start).cross(mp);
	double B = lp.cross(mp);
	if(equal(A, 0) && equal(B, 0)) return m.start; //same line
	if(equal(B, 0)) return null; //parallel
	return start.add(lp.mul(A/B));
}

線分 $S(\bar{s_s s_e})$ と線分 $T(\bar{t_s t_e})$

線分 $\bar{s_s s_e}$ を基準にして、線分 $\bar{s_s t_s}$ と線分 $\bar{s_s t_e}$ が逆方向にあり、
線分 $\bar{s_s s_e}$ に対しても、線分 $\bar{s_s t_s}$ と線分 $\bar{s_s t_e}$ が逆方向にある場合、
線分 $S$ と線分 $T$ が交差する。
平面幾何(plane geometory)で定義したccwでは、
反時計回りなら正、時計回りなら負(、同一点がある場合0)を返すはずなので、
$ccw(s_s ,s_e ,t_s)\times ccw(s_s ,s_e ,t_e)\wedge ccw(t_s ,t_e ,s_s)\times ccw(t_s ,t_e ,s_e)$ で判定できる。

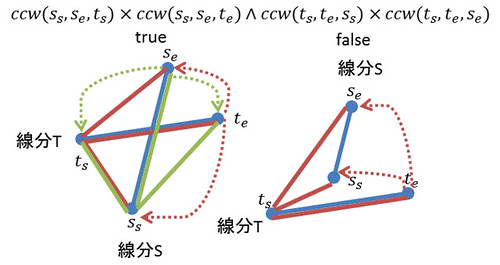
//instance method of Line class
public final boolean intersectsSS(Line t) {
	return ccw(t.start) * ccw(t.end) <= 0 && t.ccw(start) * t.ccw(end) <= 0;
}
public final Point intersectionSSPoint(Line t) {
	return intersectsSS(t) ? intersectionLLPoint(t) : null;
}

線分 $S(\bar{s_s s_e})$ と点 $\vec{p}$

頂点 $s_s, s_e, p$ について、三角不等式(triangle inequality) $d(s_s,p)+d(p, s_e) \geq d(s_e, s_s)$ を考える。
=のとき３点が一直線上にある。特に、上の式だと=のとき線分上にpがあるのが分かる。
以前作ったccwは、 $\bar{s_ss_e}$ 上に $\vec{p}$ があるとき $ccw(\vec{s_s}, \vec{s_e}, \vec{p}) = 0$ のとなるように定義したのでそれを使ってもいい。

//instance method of Point class
public final boolean intersectsPS(Line s) {
	//return s.ccw(this) == 0; //これでもおk
	return equal(s.start.distance(this) + this.distance(s.end), s.end.distance(s.start)); //三角不等式で等号が成り立つとき
}
//instance method of Line class
public final boolean intersectsSP(Point p) { return p.intersectsPS(this); }

四角形 $A(a_x , a_y, a_w, a_h)$ と四角形 $B(b_x, b_y, b_w, b_h)$

※四角形の一番左下の頂点の座標を(x,y)、四角形の幅をw, 四角形の高さを4つ組で(x, y, w, h)と表している(座標系は下図参照)。
下図より、 $a_x \leq b_x + b_w \wedge a_y \leq b_y + b_h \wedge b_x \leq a_x + a_w \wedge b_y \leq a_x + a_h$ で求まることが分る。(内包も含む)

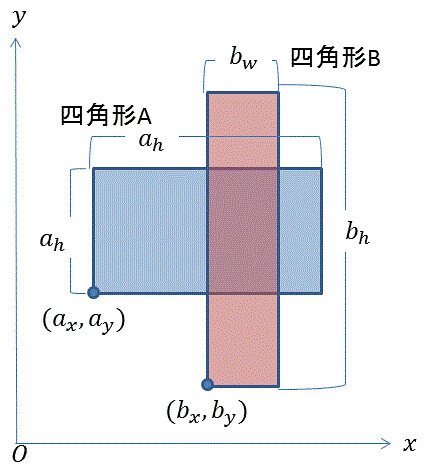
public static final boolean intersectsRR(Point[] a, Point[] b){
	return leq(a[0].x, b[1].x) && leq(a[0].y, b[1].y) && leq(b[0].x, a[1].x) && leq(b[0].y, a[1].y);
}

多角形が線分sを包含しているかどうかの判定

多角形の各辺と線分sの交点 $p_i$ を求めて、sの始点から各交点までの距離 $d_i$ を計算し、交点 $p_i$ を $d_i$ に基づいてソートする。
ソートした各交点 $p_j$ に対して $p_j$ と $p_{j+1}$ の中点を求める。
求めた中点全てが多角形の内部にあれば線分sは多角形の内部にある。

Listにsの始点から交点までの距離と交点を入れてそーとしているが、C++ならstd::vector>にいれてけばいい。
始点からの距離が同じなら、必ず同じ交点になるはずなので、Mapに入れてもよいかもしれない。

/**
 * Tests whether polygon[0]→polygon[1]→...→polygon[polygon.length-1]→polygon[0] contains segment s or not. <br>
 * @param Polygon	vertex set of target polygon
 * @param s			target segment
 * @return			true -> polygon contains s. false -> polygon doesn't contain s.
 */
public static boolean contains(Point[] polygon, Line s) {
	final int n = polygon.length;
	List<Object[]> numl = new ArrayList<Object[]>();
	numl.add(new Object[]{0., s.start});
	numl.add(new Object[]{s.distance(), s.end});
	for (int i = 0; i < n; ++i) {
		Point p = s.intersectionSSPoint(new Line(polygon[i], polygon[(i+1)%n]));
		if (p != null) numl.add(new Object[]{p.distance(s.start), p});
	}
	Collections.sort(numl, new Comparator<Object[]>(){
		@Override public int compare(Object[] o1, Object[] o2) {
			int d = Double.compare((Double)o1[0], (Double)o2[0]);
			return d != 0 ? d : ((Point)o1[1]).compareTo((Point)o2[1]);
		}
	});
	for (int i = 0; i < numl.size()-1; ++i) 
		if(!contains(polygon, ((Point)numl.get(i)[1]).add((Point)numl.get(i+1)[1]).div(2))) return false;
	return true;
}

円

public static class Circle{
	public final Point o;
	public double r;
	public Circle(double x, double y, double r){ this.o = new Point(x,y); this.r = r; }
	public Circle(Point o, double r){ this.o = new Point(o); this.r = r; }
	public void set(double x, double y, double r){ o.x = x; o.y = y; this.r = r; }
	public void set(Point o, double r){ set(o.x, o.y, r); }
//... abbr.

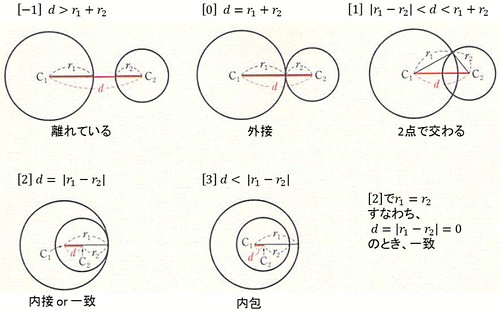
2つの円の位置関係

//instance method of class Circle
public final PosRelation positionalRelation(Circle c){
	double d2 = o.distanceSq(c.o);
	double dp2 = (r + c.r)*(r + c.r);
	if(d2 > dp2) return PosRelation.Separated;
	if(d2 == dp2) return PosRelation.Circumscribed;
	double dn2 = (r - c.r)*(r - c.r);
	if(dn2 < d2) return PosRelation.CrossAt2Point; //d < dp
	if(d2 == dn2) return PosRelation.Inscribed;
	return PosRelation.FullIncluded; //d < dn
}

点 $P(x_p, y_p)$ と円 $C(x_c, y_c, r)$

$(x_p - x_c)^2 + (y_p - y_c)^2 \leq r^2$

//instance method of Point class
public final boolean intersectsPC(Circle c){ return leq(distanceSq(c.o), c.r*c.r); }
//instance method of Circle class
public final boolean intersectsCP(Point p){ return p.intersectsPC(this); }

線分 $S(\bar{s_s s_e})$ と円 $C(x_c, y_c, r)$

平面幾何(距離)のdistanceSPで線分と円の中心の距離を求めて、それが半径以下かどうかで判定

//instance method of Line class
public final boolean intersectsSC(Circle c) { return geq(c.r, distanceSP(c.o)); }
//instance method of Circle class
public final boolean intersectsCS(Line s){ return s.intersectsSC(this); }

old ver.

多角形 $\{\vec{p_i}\}$ と円 $C(\vec{o}, r)$ の位置関係

あまりちゃんと確かめてないので要検証。線分と点の距離には、平面幾何(距離)を使う。
多角形の辺(線分)集合を $E$ とする。
$\forall p_i: d(\vec{p_i}, \vec{o})=r \rightarrow$ 外接円
$\forall p_i: d(\vec{p_i}, \vec{o})\leq \rightarrow$ 円が多角形を内包

多角形内に $\vec{o}$ が含まれる場合

$\forall \bar{e}\in E: d(\bar{e}, \vec{p}) = r \rightarrow$ 内接円
$\forall \bar{e}\in E: d(\bar{e}, \vec{p}) \geq r \rightarrow$ 多角形が円を内包
それ以外 $\rightarrow$ 一部交差

多角形内に $\vec{o}$ が含まれない

$\forall \bar{e}\in E: d(\bar{e}, \vec{p}) > r \rightarrow$ 分離
それ以外 $\rightarrow$ 一部交差

//instance method of Circle class
public PosRelation positionalRelation(final Point[] polygon){
	final int n = polygon.length;
	double[] dists = new double[n];
	boolean flag = true, eq = true;
	for(int i = 0; i < n; ++i){
		dists[i] = o.distance(polygon[i]);
		if(!equal(dists[i], r)) eq = false;
		if(greater(dists[i], r)) flag = false;
	}
	if(eq) return PosRelation.Circumcircle; //外接円
	if(flag) return PosRelation.PolygonInCircle; //円が多角形を内包する

	for(int i = 0; i < n; ++i) dists[i] = o.distancePS(new Line(polygon[i], polygon[(i+1)%n]));

	eq = flag = true;
	if(contains(polygon, o)){
		for(double d: dists){
			if(!equal(d, r)) eq = false;
			if(less(d, r)) flag = false;
		}
		if(eq) return PosRelation.Incircle; //内接円
		if(flag) return PosRelation.CircleInPolygon; //多角形が円を内包する
	}else{
		for(double d: dists) if(leq(d, r)) flag = false;
		if(flag) return PosRelation.Separated; //分離
	}
	return PosRelation.PartialCross; //一部交差
}

直線

直線と直線

線分と線分

線分と点

四角形と四角形