グラフ理論（Graph theory） - kanetaiの二次記憶装置

(無向)グラフの要素

要素が頂点(vertex), 点(point), 節点(node)の集合 $V$
辺(edge)と呼ばれる頂点の順序対の集合 $E$

隣接(adjacent) : 辺(u,v)が存在するとき頂点 $u,v$ は隣接するという。
接続(incident) : $v$ が辺 $e$ の端点(endpoint)であるとき、 $e$ は $v$ に接続するという。
多重グラフ(multigraph) : 多重辺(multiple edges)または自己ループ(roop)を含むグラフ

※多重辺やループのない多重グラフをグラフと定義している。

部分グラフ(subgraph) $G'(V',E')$ : $G(V,E), E'\subset E, V'\subset V, E'=\{(u',v')|u',v'\in V'\}$
induced subgraph $G'(V',E')$ : 両端点が $V'$ にある辺を全て $E'$ が含むならば、 $G'(V',E')$ を $V'$ によって生成された(generated)部分グラフと呼ぶ。

次数(degree)

次数(degree) : $\deg(e) = v$ に接続する辺の個数
孤立点(isolated vertex) : 次数0の頂点
- $\sum_{v\in V}\deg(v)=2$ の倍数 $\cdots (1)$

連結度(connectivity)

歩道(walk) : 多重グラフにおいて、頂点と辺の交互列 $v_0, e_1, v_1, \cdots , v_{n-1}, e_n, v_n$ 。誤解を招かないとき、辺または頂点の列で歩道を表す。辺の数 $n$ を歩道の長さという。 $v_0 = v_n$ のとき、歩道は閉じている(closed)という。
小道(trail) : すべての辺が異なる歩道
道(path) : すべての頂点が異なる歩道
閉路(cycle) : を除いたすべての頂点が異なる閉じた歩道。長さの閉路を閉路(cycle)という。
- 頂点 $u$ から頂点 $v$ への歩道が存在するとき、かつその時に限り、 $u$ から $v$ への道が存在する $\cdots (2)$

連結(connected) : グラフの任意の2頂点の間に道が存在するとき、グラフは連結であるといわれる。
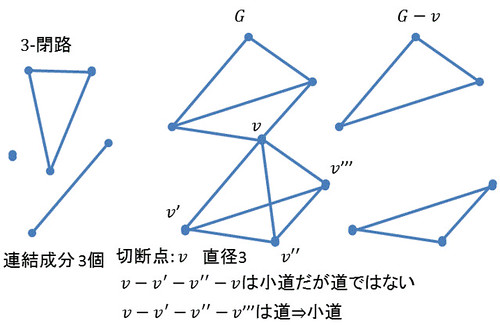
連結成分(connected component) : 連結部分グラフより大きな連結部分グラフでを含むものが存在しないときの
- 任意のグラフが、連結成分に分割することができる $\cdots (3)$

距離(distance) : $d(u,v) = u,v$ 間の最短道の長さ
直径(diameter) : $\max \{ d(u,v)\}$
$G-v$ : $G$ から $v$ と $v$ に接続しているすべての辺を除いて得られるグラフ
切断点(cut point) : $G-v$ が非連結になるときの $v$

周遊

周遊可能小道(traversable trail) : 多重グラフの全ての頂点を含み。各辺をちょうど１回だけ用いる歩道(小道)(閉じてなくもOK)
周遊可能(traversable) : 周遊可能小道が存在する状態(一筆書きができるグラフ)
オイラー小道(Eulerian trail) : 閉じた周遊可能小道
オイラーグラフ(Eulerian graph) : オイラー小道が存在するグラフ
準オイラーグラフ(semi-Eulerian graph) : 閉じてない周遊可能小道が存在するグラフ

※無向グラフの場合

- 無向有限連結グラフがオイラーグラフ⇔各頂点が偶次数を持つ(奇頂点が0個) $\cdots (4)$
- 無向有限連結グラフが準オイラーグラフ⇔奇頂点が2個。(周遊可能小道は一方の奇頂点から始まり、他方の奇頂点で終わる。) $\cdots (5)$
- ３個以上の奇頂点を持つ多重グラフは周遊可能ではない $\cdots (6)$

※奇頂点が0個の場合でも周遊可能な場合はある(オイラーグラフ)
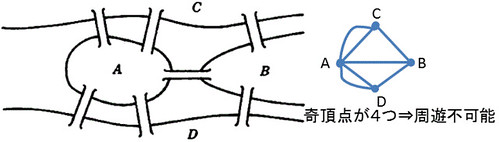
頂点Pが周遊開始・終了点でない場合、頂点Pに到達するための辺と出ていく辺が必要なのでPは偶頂点でなければならない。よって、ある点Qが奇頂点ならそこは、周遊開始または終了点でなければならない。
(6)より、ケーニヒスベルグの橋を周遊するような散歩が不可能であることがわかる。
迂回したり、水面散歩したら周遊可能ですけどね。
オイラー路(Euler Path)
同様の考え方で、有向グラフの場合は、相対入次数と相対出次数をみて判断できる。

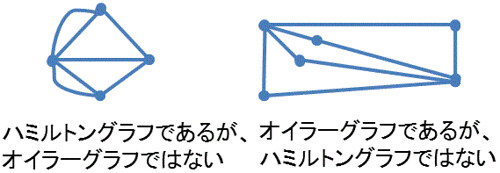
ハミルトン閉路(Hamilton cycle) : 各頂点を1回だけ含む(開始・終了点を除く)閉じた歩道(閉路)
ハミルトングラフ(Hamilton graph) : ハミルトン閉路を持つグラフ

※オイラーグラフのように単純な判定方法がない

巡回セールスマン問題(traveling salesman problem) : すべての頂点を含む最短歩道を見つける問題

特殊なグラフ

完全グラフ(complete graph) : 拡張点が他の全ての頂点と結ばれているグラフ。 $|V|=n$ なら $K_n$ で表す。
正則グラフ(regular graph) : すべての頂点が同じ次数をもつグラフ。次数がが $k$ の場合、次数 $k$ の正則(regular of degree $k$ )または、 $k-$ 正則( $k-$ regular)という。

※ $n$ 頂点の完全正則グラフは $n-1$ 次正則

2部グラフ(bipartite graph) : $V\subset M, V\subset N, M\cap N = \phi , E=\{ (m,n)|m\in M, n\in N\}$ となっている $G(V,E)$ のことで、 $k_{|M||N|}$ で表す。※ $|E|=|M||N|$
非閉路的(cycle-free), 無閉路的(acyclic) : 閉路を持たない
木(tree) : 閉路を持たない有限連結グラフ
森(forest) : 閉路を持たない有限グラフ

行列表現

辺行列(edge matrix) : 辺を縦に並べただけの $|E|\times 2$ 行列
隣接行列(adjacecy matrix) : $|V|$ 次正方行列 $A=(a_{i,j})$ .

$a_{i,j}=\left\{ \begin{array}{lr} 1 & (v_i, v_j)\in E \\ 0 & (otherwise)\end{array}\right.$
※対角成分は通常0, 多重グラフでは辺の本数、重み付きグラフでは重みを入れることがある。

接続行列(incidence matrix) : $|V|\times |E|$ 行列 $M=(m_{i,j})$

$m_{i,j}=\left\{ \begin{array}{lr} 1 & e_j = (x,v_i)\vee e_j=(v_i, x) \\ 0 & (otherwise)\end{array}\right.$

連結行列(connection matrix) : $|V|$ 次正方行列 $C=(c_{i,j})$

$c_{i,j} = \left\{ \begin{array}{lr} 1 & i=j\vee exist\ path(v_i,v_j) \\ 0 & (otherwise)\end{array}\right.$

- $A$ を $|V|>1$ 頂点から成るグラフの隣接行列としたとき、 $A^n$ の $(i,j)$ 成分は頂点 $v_i$ から頂点 $v_j$ への長さ $n$ の歩道の個数 $\cdots (7)$
- $\sum_{i=1}^{|V|-1}A^i$ は、 $path(v_i,v_j)$ が存在しないときに限り、 $(i,j)$ 成分=0になる $\cdots (8)$
- $C=\sum_{i=0}^{|V|-1}A^i$ , ただし、 $A^0 = I_{|V|}$ ( $|V|$ 次単位行列) $\cdots (9)$

同形、同相

同形写像(isomorphism) : $G(V,E), G^*(V^*,E^*)$ について、 $(f(u),f(v))\in E^*, (u,v)\in E$ となるような1対1写像 $f:V\mapsto V^*$
同形(isomorphic) : $G(V,E)$ が $G^*(V^*,E^*)$ に同形写像されているとき、 $G(V,E),G^*(V^*,E^*)$ を同形という。
同相(homeomorphic) : ２つのグラフ $G,G^*$ の辺の端点の間のどこかに、頂点を追加することで、同形なグラフが得られるとき、 $G$ と $G^*$ は同相であるという。

有向グラフ(directed graph, digraph)