魔方陣(magic square)

参考ページ

• 魔方陣 - Wikipedia
• http://www2u.biglobe.ne.jp/~zed/m_stitle.htm

魔方陣(magic square)

正方形で縦・横・斜の数字の合計がすべて等しい方陣。
特に、(次)の行列の方陣の要素として()を重複なく使用したものを魔方陣と呼ぶことが多い。
その場合、
縦or横or斜の数字の合計は
2次の魔方陣は1,2,3,4を使う限り存在しない
octave 3.2.4のmagic()関数と同じアルゴリズムの魔方陣を作ってみた。
octaveのmagic()関数は、奇数、4の倍数、2を除く4の倍数以外の偶数でアルゴリズムが異なる.

static int[][] magicSquare(int n) throws Exception{
	if(n<=0 || n==2) throw new Exception();
	if(n % 2 == 1) return magicSquareOdd(n);
	if(n % 4 == 0) return magicSquareDoubleEven(n);
	return magicSquareSingleEven(n);
}

奇数の場合()

1行目中央から初めて右斜め上にインクリメントしていく
上に行き過ぎたり右に行き過ぎたりしたら、下、左から出てくる。
既に書き込んでいるところまでたどり着いたらその下から、同じように右斜め上にインクリメントしていく

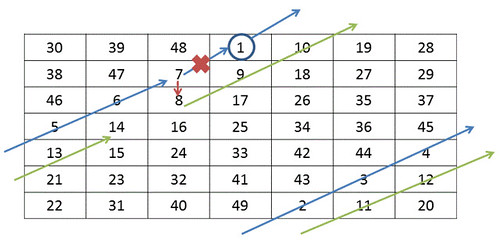
コードは下の通り、
%nで上下、左右の巡回を表現する。
初めのnは引き算で負の値にならないようにするためのバイアス。
行インデックスの2*iは、右斜めに進んで行って、すでに書き込んでいるところにたどり着いたとき、
その下(要素1から下に2*i)の位置を示す。-jで上に進む。
列インデックスのn/2は初めの位置(中央)を示す。
-iは、右斜めに進んで行って、すでに書き込んでいるところにたどり着いたとき、
その下(要素1から←にi)の位置を示す。+jで右に進む。

static int[][] magicSquareOdd(int n){
	int[][] M = new int[n][n];
	int k = 1;
	for(int i = 0; i < n; ++i)
		for(int j = 0; j < n; ++j)
			M[(n+2*i-j)%n][(n+n/2-i+j)%n] = k++;
	return M;
}

ちなみに、魔方陣 | Aizu Online Judgeで作った魔方陣はこんな感じ

int k = 0;
int[][] a = new int[n][n];
for(int i = -n/2; i <= n/2; ++i)
	for(int j = 0; j < n; ++j)
		a[(j+i+n)%n][(j-i+n)%n] = ++k;

4の倍数の場合()

下図に示すパターンのように、2個ずつ上下からインクリメントしていく

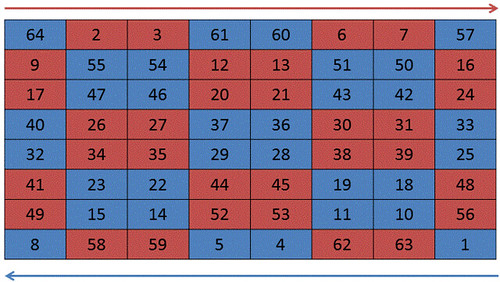
static int[][] magicSquareDoubleEven(int n){
	int[][] M = new int[n][n];
	int x, y, k = 1;
	for(int i = 0; i < n; ++i){
		for(int j = 0; j < n; ++j){
			x = i % 4;
			if(x==1 || x==2) y=(j+2)%4;
			else y = j%4;
			if(y==1 || y==2) M[i][j] = k++;
			else M[n-1-i][n-1-j] = k++;
		}
	}
	return M; 
}

2を除く4の倍数でない偶数()

octaveのmagic関数の規則性がよくわからなかったので、magic関数を実装しているmファイルの中身を見てみたが、
あまりピンとこない

m = n/2;
A = magic (m);
A = [A, A+2*m*m; A+3*m*m, A+m*m];
k = (m-1)/2;
if (k>1)
  I = 1:m;
  J = [2:k, n-k+2:n];
  A([I,I+m],J) = A([I+m,I],J);
endif
I = [1:k, k+2:m];
A([I,I+m],1) = A([I+m,I],1);
I = k + 1;
A([I,I+m],I) = A([I+m,I],I);

これをjavaで書いたのがこれ

public static int[][] swap(int[][] M, int i, int j, int k, int l){
	int temp = M[i][j]; M[i][j] = M[k][l]; M[k][l] = temp;
	return M;
}
static int[][] magicSquareSingleEven(int n){
	int[][] M = new int[n][n];
	int m = n/2;
	int m2 = m*m;
	int k = (m-1)/2;
	int[][] A = magicSquareOdd(m);
	for(int i = 0; i < m; ++i){
		for(int j = 0; j < m; ++j){
			M[i][j] = M[i+m][j] = M[i][j+m] = M[i+m][j+m] = A[i][j];
			M[i+m][j+m] += m2;
			M[i][j+m] += 2*m2;
			M[i+m][j] += 3*m2;
		}
	}
	if(k>1){
		for(int i = 0; i < m; ++i){
			for(int j=1; j < k; ++j){
				swap(M, i,j, i+m,j);
				swap(M, i,n-k+j, i+m,n-k+j);
			}
		}
	}
	for(int i=0; i < k; ++i){
		swap(M, i,0, i+m,0);
		swap(M, i+k+1,0, i+k+1+m,0);
	}
	swap(M, k,k, k+m,k);
	return M;
}

一応これで、Octaveと同じmagic関数が作れるが、
単に次の魔方陣を作りたいなら魔方陣 - WikipediaのLUX法の方がわかりやすい(上の実装もこれの変形版になっているのかもしれないが、よくわからなかった)。