いろいろメモ
メモ
後でまとめる
作業ディレクトリとrev
svn diff -x -b -r 4117
intersectSC old ver.
とする。
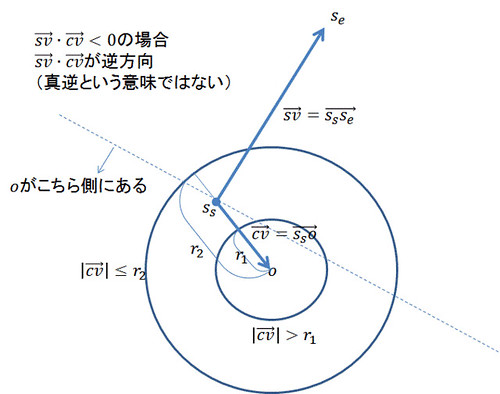
-
の場合
なら交差、
なら非交差
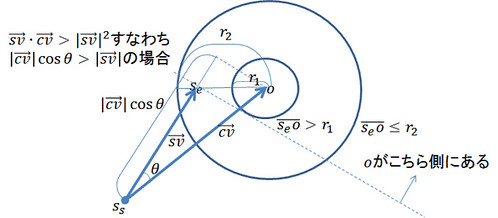
-
かつ
の場合
なら交差、
なら非交差
-
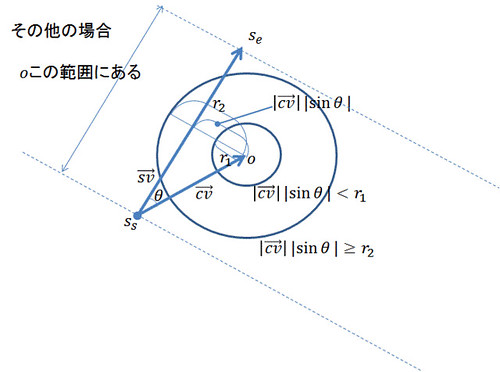
- その他の場合
なら交差、
なら非交差
- その他の場合
//instance method of Line class public final boolean intersectsSC(Circle c){ Point cv = c.o.sub(start), sv = end.sub(start); double d0 = sv.dot(cv); if(less(d0, 0)) return leq(cv.norm(), c.r); if(greater(d0, sv.normsq())) return leq(end.distanceSq(c.o), c.r * c.r); return leq(cv.normsq() - (d0/sv.normsq()) * d0, c.r * c.r); }