平面幾何(射影、鏡映)

正射影(orthograph, orthogonal projection)　射影(projection)、鏡映(reflection)

一点からある直線または平面上に下ろした垂線の交点(垂線の足:foot of a perpendicular)。図形(点の集合)についても、図形上のすべての点の垂線の足の集合を正射影と呼ぶ。
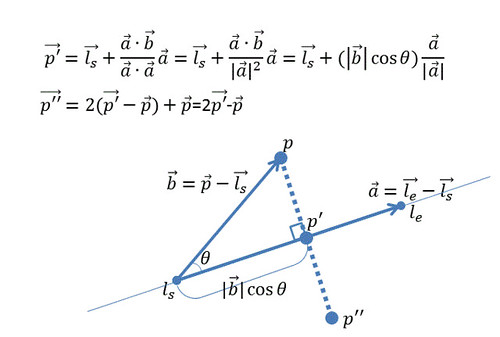
、と置くと点の直線への正射影は、

また、点の直線に対する鏡映は、

//instance method of Point class
public final Point projection(Line l){
	Point a = l.end.sub(l.start);
	Point b = this.sub(l.start);
	return l.start.add(a.mul(a.dot(b)/a.normsq()));
}
public final Point reflection(Line l){ return projection(l).mul(2).sub(this); }
//instance method of Line class
public final Point projection(Point p){ return p.projection(this); }
public final Point reflection(Point p){ return p.reflection(this); }