Fenwick tree, binray indexed tree(BIT) - kanetaiの二次記憶装置

リポジトリ
 Fenwick tree, binray indexed tree(BIT)
$x_0, x_1, \cdots , x_{n-1}$
が与えられたとき、

$O(\log n)$ 累積和 $sum(k)=\sum_{i=0}^k x_i$
$O(\log n)$ 加算更新 $add(i, a)=x_{i}\leftarrow x_{i}+a$

の操作ができるデータ構造で、空間計算量は $O(n)$ 、構築にかかる計算量は(n回addするので) $O(n\log n)$ 。
当然だが(頻繁に)更新を行わないのであれば、普通に $S_i = x_i + S_{i-1}$ でテーブル作った方がいい。

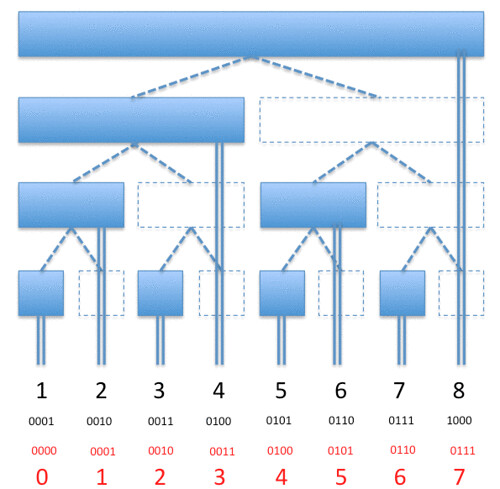
葉が $x_0, x_1, \cdots , x_{n-1}$ に相当する。親は子の要素を足した値を保持する。
ここで、下図の点線のノードは不要で使用せず、実線のノードだけを使う。
葉の下の数字はノード番号(1スタートさせることも多々あるが、実装は0スタートの物にした)。
累積和 $sum(k)$ は、ノード $k$ から左上のノードを足していく。
加算更新 $add(i,a)$ は、ノード $i$ から親ノードに $a$ を順次加えていく。

実装は非常にラク。インデクスを1スタートにすると、カレントノードの遷移が(j&-j)を加算/減算するだけで分かりやすい。
ちなみに(j&-j)は、２進数表示で考えたとき、jの下位bit(右)から見て一番始めに1がたっているところだけ1それ以外は0の数。

public final class FenwickTree{
	private int[] x;
	public FenwickTree(int n){ init(n);}
	public FenwickTree(int[] x){ init(x, 0, x.length);}
	public FenwickTree(int[] x, int begin, int end){ init(x, begin, end); }
        /** all 0, O(n) n:=x.length */
	public final void init(int n){ x = new int[n]; Arrays.fill(x, 0); }
	/** O(n log n) n:=x.length */
	public final void init(int[] x){ init(x, 0, x.length); }
	/** O(n log n) n:=x.length */
	public final void init(int[] x, int begin, int end){
		this.x = new int[end - begin];
		System.arraycopy(x, begin, this.x, 0, end - begin);
	}
	/**
	 * Gets summation from x[0] to x[i] O(log n) n:=x.length<br>
	 * @param i	(inclusive) end index
	 * @return	x[0] + x[1] + ... + x[i]
	 */
	public final int sum(int i){
		int ret = 0;
		//If 1 start (not 0 start), use j -= (j&-j)
		for(int j = i; j >= 0; j = ((j & (j+1)) - 1)) ret += x[j];
		return ret;
	}
	/**
	 * Gets summation from x[i] to x[j] (※i <= j) O(log n) n:=x.length
	 * @param i (inclusive) start index
	 * @param j (inclusive) end index
	 * @return  x[i] + x[i+1] + ... + x[j]
	 */
	public final int sum(int i, int j){ return i == 0 ? sum(j) : sum(j) - sum(i-1); }
	/**
	 * x[i] += a O(log n) n:=x.length<br>
	 * @param i target index
	 * @param a	
	 */
	public final void add(int i, int a){
		//If 1 start (not 0 start), use j += (j&-j)
		for(int j = i; j < x.length; j |= j+1) x[j] += a;
	}
}