Cats Going Straight II(AOJ No.0273)

まっすぐな壁で囲まれたいくつかの部屋からなるお屋敷がある。
お屋敷の一番外側の壁をみると、凸多角形になっている。
１枚の壁はその両端にある柱によって支えられている。

異なる柱が同じ位置を占めることはない。
異なる壁が重なったり、柱以外で交差することはない。
１つの柱は２つ以上の壁を支えている。
壁の長さは 0 より大きい。
柱は壁の両端だけにある。つまり、柱が壁の途中にあることはない。
壁は異なる２つの部屋、あるいは部屋と外とを仕切る。
任意の異なる２つの柱を選んだとき、互いの柱には壁をたどって到達できる。

お屋敷の部屋のどこかに猫がおり、猫は壁をすり抜けることができる。
猫が「最良の選択」をした場合、外に出るまでに通る穴の数の最大値を求める。
制約
-1000 ≤ 座標 ≤ 1000
3 ≤ 柱の数、壁の数 ≤ 100

アルゴリズム

双対グラフを作って、BFSで外に相当するノードから各部屋に相当するノードへの距離(ホップ数)を求める。

双対グラフを作るにはまず、領域を求めなければならない。
双方向の有向グラフを考え、各辺を半時計回りにソートした隣接リストで元のグラフを表現する。
半時計回りにソートするには、始点から終点への方向ベクトルの偏角 $[ -\pi, \pi]$ の昇順にソートすれば良い。
そして、有向辺に属す領域を示す色を塗っていく。
色が塗られていない有向辺に色を割り当てて、その逆辺から半時計回りにある辺に同じ色を塗る。これを繰り返してもとの有向辺にもどってきたら一つ領域分の色が塗り終わる。これを全てのアークに色がつくまで行うとすべての領域が求まる。
最後にある有向辺とその逆辺の領域(色)を結ぶと双対グラフができる。

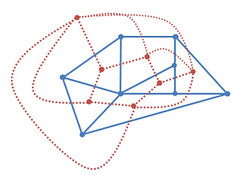
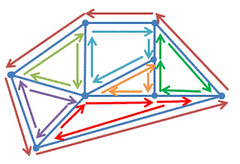
元の(彩色済みの有向)グラフでは、一番左のノードからでる有向辺のうち一番偏角が小さい（ $-\pi$ に近い）有向辺が外に対応する色が塗られている。
それに対応する双対グラフのノードからDFSを行う。ホップ数の最大値が答え。

コード

Edgeの情報として、終点ノードのインデックス、始点から終点への方向ベクトルの偏角、(ソート済みのリストでの)逆辺のインデックス、色（領域）を持たせた。
偏角はMath.atan2を使って求める。

import java.util.*;
import java.awt.Point;
public class aoj0273 {
	static final Scanner stdin = new Scanner(System.in);
	static Point[] points;
	public static void main(String[] args) {
		while (true) {
			int n = stdin.nextInt(), W = stdin.nextInt();
			if ((n|W) == 0) break;
			points = new Point[n];
			for (int i = 0; i < n; ++i) points[i] = new Point(stdin.nextInt(), stdin.nextInt());
			List<List<Edge>> adjList = new ArrayList<List<Edge>>(n);
			for (int i = 0; i < n; ++i) adjList.add(new ArrayList<Edge>());
			while (W-- > 0) {
				int src = stdin.nextInt()-1, dst = stdin.nextInt()-1;
				adjList.get(src).add(new Edge(src, dst)); adjList.get(dst).add(new Edge(dst, src));
			}
			boolean[][] adjMatrix = buildDualGraph(adjList, n);
			int mi = 0, mx = points[mi].x;
			for (int i = 1; i < n; ++i) if (mx > points[i].x) { mi = i; mx = points[i].x; }
			int out = adjList.get(mi).get(0).region;
			
			n = adjMatrix.length;
			int[] dist = new int[n];
			Arrays.fill(dist, -1);
			Queue<Integer> q = new LinkedList<Integer>();
			q.add(out);
			dist[out] = 0;
			while (!q.isEmpty()) {
				int p = q.poll();
				for (int r = 0; r < n; ++r) if (adjMatrix[p][r] && dist[r] == -1) {
					dist[r] = dist[p] + 1;
					q.add(r);
				}
			}
			int ans = -1;
			for (int d : dist) ans = Math.max(ans, d);
			System.out.println(ans);
		}
	}
	static boolean[][] buildDualGraph(List<List<Edge>> adjList, int n) {
		for (List<Edge> l : adjList) Collections.sort(l);
		for (int i = 0; i < n; ++i) for (Edge e : adjList.get(i)) {
			int idx = -1;
			while (adjList.get(e.dst).get(++idx).dst != i);
			e.rev = idx;
		}
		int regionID = 0;
		for (int i = 0; i < n; ++i) for (int j = 0; j < adjList.get(i).size(); ++j) 
			if (adjList.get(i).get(j).region == -1) setRegion(adjList, i, j, regionID++);
		boolean[][] adjMatrix = new boolean[regionID][regionID];
		for (List<Edge> l : adjList) for (int j = 0, k = l.size()-1; j < l.size(); k = j++) {
			int src = l.get(k).region, dst = l.get(j).region;
			adjMatrix[src][dst] = adjMatrix[dst][src] = true;
		}
		return adjMatrix;
	}
	static void setRegion(List<List<Edge>> adjList, int i, int j, int regionID) {
		while (true) {
			Edge e = adjList.get(i).get(j);
			int ni = e.dst, nj = (e.rev + 1) % adjList.get(ni).size();
			Edge ne = adjList.get(ni).get(nj);
			if (ne.region != -1) break;
			ne.region = regionID;
			i = ni; j = nj;
		}
	}
	static class Edge implements Comparable<Edge> {
		int region = -1, dst, rev;
		double arg;
		Edge(int src, int dst) { 
			this.dst = dst;
			this.arg = Math.atan2(points[dst].y - points[src].y, points[dst].x - points[src].x);
		}
		@Override public int compareTo(Edge o) { return Double.compare(this.arg, o.arg); }
	}
}