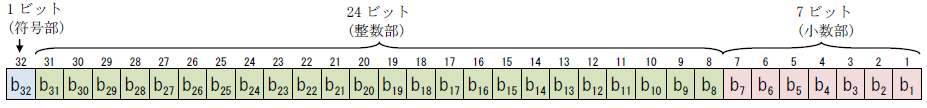kanetaiの二次記憶装置

プログラミングに関するやってみた、調べた系のものをQitaに移して、それ以外をはてブでやる運用にしようと思います。http://qiita.com/kanetai

Aka-beko and 40 Thieves(AOJ No. 0266), Triangle of Blocks(AOJ No. 0267), Kongo Type(AOJ No. 0268), East Wind(AOJ No. 0269), Modular Query(AOJ No. 0270)

Online judge

リポジトリ

Aka-beko and 40 Thieves(AOJ No.0266)

http://judge.u-aizu.ac.jp/onlinejudge/IMAGE2/akabeko.png
1 or 2の系列が与えられたとき、AからBに行けるかどうかを答える。

コード

import java.util.*;
public class aoj0266 {
	static final Scanner stdin = new Scanner(System.in);
	enum City { 
		A, B, X, Y, Z, W, D;
		static City path[][] = { {X, Y}, {Y, X}, {D, Z}, {X, D}, {W, B}, {B, Y}, {D, D} };
	}
	public static void main(String[] args) {
		while (true) {
			char[] str = stdin.next().toCharArray();
			if (str[0] == '#') break;
			int pos = City.A.ordinal();
			for (char c : str) pos = City.path[pos][c - '0'].ordinal();
			System.out.println(pos == City.B.ordinal() ? "Yes" : "No");
		}
	}
}

Triangle of Blocks(AOJ No. 0267)

ブロックの並びが与えられたとき

  • 一番下のブロックを取り除く
  • 取り除いたブロックを右端に縦に並べる。
  • 隙間がある場合は右につめる

という操作を何回繰り返せば段差１の階段状になるかを答える。完成系にならない場合または操作回数が10,000を超える場合はNAと答える。
階段の高さをkとしたときブロックの総数がk×(k＋1)/2でないと完成系はつくれない。

コード

import java.util.*;
public class aoj0267 {
	static final Scanner stdin = new Scanner(System.in);
	static final int LIMIT = 10000, N = 100;
	@SuppressWarnings("serial") static final List<Integer> TRI = new ArrayList<Integer>(N){
		{ add(-1); for (int i = 0; i < N; ++i) add((i+1)*(i+2)/2); }
	};
	public static void main(String[] args) {
		while (true) {
			int n = stdin.nextInt(), s = 0;
			if (n == 0) break;
			List<Integer> l = new ArrayList<Integer>(n);
			for (int i = 0; i < n; ++i) {
				l.add(stdin.nextInt());
				s += l.get(i);
			}
			int i = -1;
			if (TRI.contains(s)) {
				for (i = 0; i <= LIMIT &&  !check(l); ++i) {
					int sz = l.size();
					for (int j = 0; j < sz; ++j) l.set(j, l.get(j)-1);
					int idx = -1;
					while((idx = l.indexOf(0)) != -1) l.remove(idx);
					l.add(sz);
				}
			}
			System.out.println(i > LIMIT ? -1 : i);
		}
	}
	static boolean check(List<Integer> l) {
		for (int i = 0; i < l.size(); ++i) if (l.get(i) != i+1) return false;
		return true;
	}
}

Kongo Type(AOJ No. 0268)

金剛型：
http://judge.u-aizu.ac.jp/onlinejudge/IMAGE2/kongoType1.png
金剛型２進数を１０進数で一切の誤差無く出力する。

コード

BigDecimal使わなくてもいいかも

import java.math.BigDecimal;
import java.util.*;
public class aoj0268 {
	static final Scanner stdin = new Scanner(System.in);
	static final BigDecimal divisor = new BigDecimal((1<<7));
	public static void main(String[] args) {
		int n = stdin.nextInt();
		while (n-- > 0) {
			long x = Long.parseLong(stdin.next(), 16);
			StringBuilder sb = new StringBuilder((x&0x80000000) == 0 ? "" : "-");
			BigDecimal d = new BigDecimal((x&0x7fffffff));
			sb.append(d.divide(divisor).toString());
			if (sb.indexOf(".") == -1) sb.append(".0");
			System.out.println(sb.toString());
		}
	}
}

East Wind(AOJ No. 0269)

座標(0,0)に私の梅の木があり、
まず、H個の家、U個の（私のではない）梅の木、M個の松の木、S個の桜の木の座標と、梅・桃・桜の香りが広がる角度du、dm、dsが与えられる。
風の強さaと風の吹く方向wが与えられたとき、図のように香りが広がる。
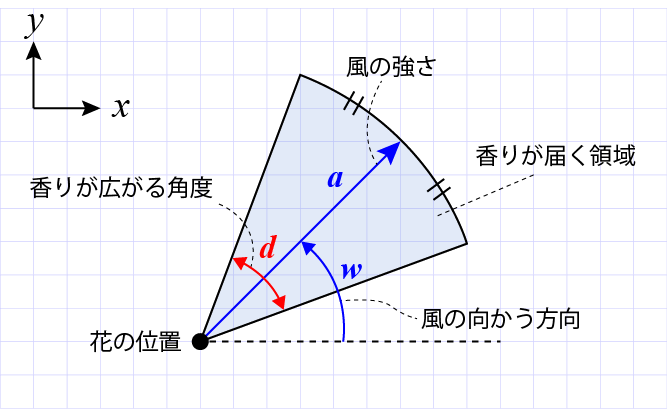
http://judge.u-aizu.ac.jp/onlinejudge/IMAGE2/kochi.png
R日分の風の情報(風の強さ+風の方向)が与えられたとき、私の梅の木の香りだけがとどく日数が最も多い家を答える。
候補が多い場合は、家を昇順にならべて答える。
制約
1 ≤ H,R ≤ 100)

  • 1,000 ≤ 座標 ≤ 1,000 以下の整数である。

0 ≤ w < 360, 1 ≤ du,dm,ds < 180 （単位は°）
0 < a ≤ 100
0 ≤ U, M, S ≤ 10

アルゴリズム

香りの境界の方向ベクトルを
\vec{d_1} = [\cos (w-\frac{d}{2}) , \sin (w-\frac{d}{2})]^T, \vec{d_2} = [\cos (w+\frac{d}{2}), \sin (w+\frac{d}{2})]^T
木から家への方向ベクトルを \vec{p}
としたとき、距離がa以内かつ、 \vec{p}が \vec{d_1}からccw, \vec{d_2}からcwの位置にあれば香りがその家にとどく。
ccwかcwかは外積の符号で決めればいい。

コード

Math.toRadiansの存在に初めて気付いた。

import java.awt.geom.Point2D;
import java.util.*;
public class aoj0269 {
	static final Scanner stdin = new Scanner(System.in);
	public static void main(String[] args) {
		while (true) {
			int H = stdin.nextInt(), R = stdin.nextInt();
			if ((H|R) == 0) break;
			Point[] house = new Point[H];
			for (int i = 0; i < H; ++i) house[i] = new Point(stdin.nextDouble(), stdin.nextDouble());
			T[][] t = new T[3][];
			t[0] = new T[stdin.nextInt()];
			t[1] = new T[stdin.nextInt()];
			t[2] = new T[stdin.nextInt()];
			int[] ds = {stdin.nextInt(), stdin.nextInt(), stdin.nextInt()};
			for (int i = 0; i < t.length; ++i)
				for (int j = 0; j < t[i].length; ++j) t[i][j] = new T(stdin.nextInt(), stdin.nextInt(), ds[i]);
			T myU = new T(0, 0, ds[0]);
			int freq[][] = new int[H][2];
			for (int i = 0; i < H; ++i) freq[i][1] = i+1;
			for (int k = 0; k < R; ++k) {
				int w = stdin.nextInt(), a = stdin.nextInt();
				myU.input(w, a);
				for (int i = 0; i < t.length; ++i) for (int j = 0; j < t[i].length; ++j) t[i][j].input(w, a);
				LOOP: for (int h = 0; h < H; ++h) {
					if (!myU.contain(house[h])) continue;
					for (int i = 0; i < t.length; ++i) for (int j = 0; j < t[i].length; ++j) 
						if (t[i][j].contain(house[h])) continue LOOP;
					freq[h][0]++;
				}
			}
			Arrays.sort(freq, new Comparator<int[]>(){
				@Override public int compare(int[] o1, int[] o2) {
					return o1[0] != o2[0] ? o2[0] - o1[0] : o1[1] - o2[1];
				}
			});
			StringBuilder sb = new StringBuilder();
			if (freq[0][0] == 0) {
				sb.append("NA");
			} else { 
				sb.append(freq[0][1]);
				int m = freq[0][0];
				for (int i = 1; i < H; ++i) {
					if (freq[i][0] == m) sb.append(" ").append(freq[i][1]);
					else break;
				}
			}
			System.out.println(sb.toString());
		}
	}
	static class T {
		Point[] tri = new Point[3];
		int d, a;
		T(int x, int y, int d) {
			this.d = d;
			tri[0] = new Point(x, y);
		}
		void input(int w, int a) {
			this.a = a;
			double theta = Math.toRadians(w-d/2);
			tri[1] = new Point(Math.cos(theta), Math.sin(theta));
			theta = Math.toRadians(w+d/2);
			tri[2] = new Point(Math.cos(theta), Math.sin(theta));
		}
		boolean contain(Point p) { 
			return leq(p.distance(tri[0]), a) && 
				leq(0, tri[1].cross(p.sub(tri[0]))) && leq(0, p.sub(tri[0]).cross(tri[2]));
		}
	}
	public static final double EPS = 1e-9;
	public static boolean leq(double a, double b){ return a - b < EPS; }			// a <= b
	@SuppressWarnings("serial") public static class Point extends Point2D.Double {
		public Point(double x, double y){ super(x,y); }
		public final Point sub(Point p){ return new Point( x - p.x, y - p.y ); }
		public final double cross(Point p){ return x * p.y - y * p.x; }
	} //class Point
}

Modular Query(AOJ No. 0270)

N個の整数ci, とQ個の整数(クエリ)qjが与えられ、各クエリごとに \max_i \{ c_i \bmod q_j\} を答える。
制約
2 ≤ N ≤ 300,000
2 ≤ Q ≤ 100,000
1 ≤ ci, q_j ≤ 300,000
q_j \neq q_{j'}, j\neq j'

アルゴリズム

cを入力した後、LB[k] = lower_bound(c, c+N, k-1)を求めとく(kより小さい最大のci).
qが与えられると、LB[max(c)]からLB[1]の方向へ探索する。
ci = kだったとき、剰余p = ci % qjを求めて解答候補を更新(最大値を保存)する。
次の探索位置は、k-pより小さい最大のci。
k' = LB[k-p]の位置にスキップして探索する。
これを繰り返すと O(\sum_j \frac{\max_i \{ c_i \} }{q_j})で求まる。
qが大きく、ciが密集しているときに効率がよくなる。

コード

import java.util.*;
public class aoj0270 {
	static final Scanner stdin = new Scanner(System.in);
	static final int N = 300001, LB[] = new int[N];
	static final boolean C[] = new boolean[N];
	public static void main(String[] args) {
		int n = stdin.nextInt(), Q = stdin.nextInt(), m = -1;
		for (int i = 0; i < n; ++i) { int c = stdin.nextInt(); C[c] = true; m = Math.max(m, c); }
		for (int i = 0, j = 0; i < m+1; ++i) { LB[i] = j; if (C[i]) j = i; }
		while (Q-- > 0) {
			int q = stdin.nextInt(), ans = 0, p;
			for (int i = m; i > 0; i = LB[i-p]) {
				p = i % q;
				ans = Math.max(ans, p);
				if (i - p < 0) break;
			}
			System.out.println(ans);
		}
	}
}