kanetaiの二次記憶装置

プログラミングに関するやってみた、調べた系のものをQitaに移して、それ以外をはてブでやる運用にしようと思います。http://qiita.com/kanetai

macでHaskell環境構築メモ

Haskell IDE

動機

新言語Swiftとか色々な言語でで関数型プログラミングをサポートし始めたので、ちょっとかじっておきたかった。
学ぶなら純粋関数型言語ということで、言語はHaskellにしますた。
プログラミングHaskell
参考書はプログラミングHaskell。
訳者のサポートページhttp://www.mew.org/~kazu/doc/book/haskell.html

中古で買ったので、結構書き込みがあった。
ざっと読んだかんじだと、他言語の入門書のような感じではなく、
少しアカデミックな（高専とか大学で使う教科書のような）感じ。
（他のHaskellの本がどんな感じかは知りませんが）
まだ、そんなに読んでませんが日本語訳は非常に読みやすいです。

コンパイル　実行環境

コンパイラ

GHC(Glasgow Haskell Compiler)というのが主流っぽい。
バイナリ（コンパイラ）とインタラクティブシェル（インタプリタ）両方ある。
Hugsというのもあるけどこちらはインタプリタだけで軽量らしい。

brew update
brew upgrade
brew install ghc haskell-platform

↑を試みたがビルドで失敗してるっぽい。
Marvericksだとgccがclangのエイリアスになってたような気がしたので、

brew install https://raw.github.com/Homebrew/homebrew-dupes/master/apple-gcc42.rb
alias gcc=gcc-4.2

を試したが、駄目でした。
適当にググって他に依存してそうなものをインストールし直してみたけどやはり駄目。

結局、http://www.haskell.org/platform/mac.html においてあるpkgをDLしてインスコ。
はじめからそうすれば良かった...
パッケージと同じページにclangの件対処用スクリプトがあるので↓みたいな感じで実行

sudo cp ghc-clang-wrapper <mydir> #<mydir>=/usr/binとか
cd <mydir>
sudo chmod 0755 ghc-clang-wrapper
sudo ghc-clang-wrapper
動作テスト

コンソールで実行できるかテスト.
ghciでインタラクティブに実行できる。
おわるときは:quit.
とりあえず、お決まりのハロワ。行ったこと無いけど。

$ ghci
GHCi, version 7.6.3: http://www.haskell.org/ghc/  :? for help
Loading package ghc-prim ... linking ... done.
Loading package integer-gmp ... linking ... done.
Loading package base ... linking ... done.
Prelude> "Hello Work"
"Hello Work"
Prelude> :quit
Leaving GHCi.

Haskell IDE

Eclipseが既に入ってあったので、eclipseFP(Functional programming support for Eclipse) を使ってみた。
新しいソフトウェアのインストールから　http://eclipsefp.sf.net/updates　を入力してインストール。
プロジェクトを作って、src/Main.shにハロワを書いて実行してみる

main = print("Hello Work.")

コンソールでmainと打つと、ハロワが表示される。
めでたし。めでたし。

Eclipse以外にもいくつかIDEがあるけど（そっちの方がメジャー？）
とりあえず動かしたいだけだったのでeclipseFPだけでいいかな。

最大流問題(Maximum Flow Problem)

Algorithm

最小費用流問題を特殊化。
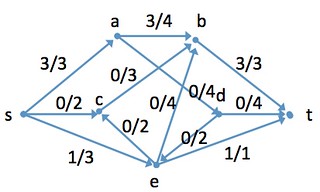
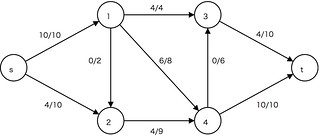
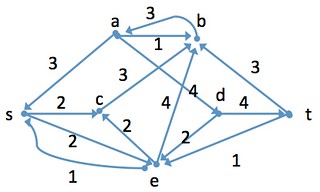
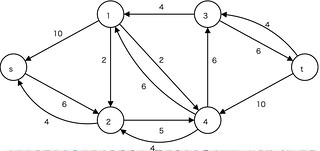
ソース節点sが複数ユニットを配布節点w経由でシンク節点に到達するように流す。各辺には、容量と実際のフローが付随する。
目標：ネットワークフローFを最大にする

コード

残余ネットワークから増加パスを求める系のアルゴリズムを使う場合に必要な、
求めた各辺のフローと最大フローと、増加パスのバックポインタ等。
列挙型でアルゴリズムを作ることにした。

public interface MaximumFlowSolver {
	public class Result {
		final int[][] capacity, flow;
		final int[] trace;
		public int maximumFlow;
		public Result(final List<List<Edge>> adjList) {
			int n = adjList.size();
			capacity = new int[n][n]; flow = new int[n][n]; trace = new int[n];
			maximumFlow = 0;
			for (final List<Edge> row : adjList) for (final Edge e : row) capacity[e.s][e.d] += e.w;
		}
		protected int residualCapacity(int src, int dst) {
			return capacity[src][dst] - flow[src][dst];
		}
	}
	public Result solve(final List<List<Edge>> adjList, int s, int t);
}

public enum MaximumFlowAlgorithm implements MaximumFlowSolver {
	Algorithm1 { 
               @Override public Result solve(List<List<Edge>> adjList, int s, int t){/*...*/}
        } /*,Algorithm2 { 
             ....
        }*/;
}

Ford-Fulkerson algorithm

増加パスPを(DFSで)見つけて、P上の辺の残余容量の最小値分のフローを増加させる。
最大流最小カット定理より増加パスPが存在しなくなった時点で最大フローとなる。
1回の増加パスで少なくともフローが1増えるとすると、whileループの繰り返しは高々 F_{\max}回。
増加パスPはO(|E|)で求まり、他の操作もO(|E|)で計算できるので、
Ford-Fulkerson algorithmの計算量は O(|E|F_{\max}).
※容量が実数だと無限ループして求まらない場合がある。
→容量は非負の整数である必要がある。(実は負でも良い?)
Algorithm Ford-Fulkerson (G=(V,E),s,t)
1: 　for ( (u,v) \in E) {
2: 　　　　 f(u,v):=0; f(v,u):=0;
3: 　}
4: 　while (増加パスPが存在する) {
5: 　　　　 c_P:= \min \{ c_f(u,v) |(u,v)\in P \}
6: 　　　　for ( (u,v)\in P) { //augment flow.
7: 　　　　　　　 f(u,v):= f(u,v)+c_P;
8: 　　　　　　　 f(v,u):= -f(u,v);
9: 　　　　}
10:　}
※ \sum_{e\in \delta^+(s)}f(e) = F_{\max}になっている。

Edmonds-Karp algorithm

Ford-Fulkerson algrithmの増加パスの求め方を限定したもの。
最短(ホップ数)となる増加パスをBFSで求める。
一つの辺が臨界辺するには、高々O(|V|)回行使すればよいので、
増加パスを求める回数はO(|V||E|).
従ってEdmonds-Karp algorithmの計算量は O(|V||E|^2)となる。
参考http://www.comp.cs.gunma-u.ac.jp/~koichi/ALG2/7.4.pdf
※容量が非負の実数であれば必ず停止する(整数でなくても良い?)
※下のコードだとnew Result()で隣接行列の生成コスト O(|V|^2)が発生している。

EdmondsKarp { /** O(|V||E|^2) */
	@Override public Result solve(List<List<Edge>> adjList, int s, int t) {
		Result res = new Result(adjList);
		while (augmentingPathExists(res, adjList, s, t)) {
			int cp = INF;
			for (int j = t; res.trace[j] != j; j = res.trace[j])
				cp = Math.min(cp, res.residualCapacity(res.trace[j], j));
			for (int j = t; res.trace[j] != j; j = res.trace[j]) {
				res.flow[res.trace[j]][j] += cp;
				res.flow[j][res.trace[j]] -= cp;
			}
			res.maximumFlow += cp;
		}
		return res;
	}
	private boolean augmentingPathExists(final Result res, final List<List<Edge>> adjList, int s, int t) { //BFS
		Arrays.fill(res.trace, -1);
		Queue<Integer> q = new LinkedList<Integer>();
		q.add(s); res.trace[s] = s;
		while (!q.isEmpty() && res.trace[t] == -1) {
			int u = q.poll();
			for(final Edge e : adjList.get(u)) if (res.trace[e.d] == -1 && res.residualCapacity(u, e.d) > 0) {
				res.trace[e.d] = u;
				q.add(e.d);
			}
		}
		return (res.trace[t] >= 0); // trace[x] == -1 <=> t-side
	}
}

Dinic's(Dinitz')algorihtm

層別ネットワークをBFS O(|E|)で作成し、DFSで流せるだけ流してブロッキングフローを作るというステップを繰り返す。
１ステップあたりのDFSによるフローの増加に要する計算量はO(|V||E|).※層別ネットワーク上でsからtへのホップ数<|V|
ブロッキングフローを流すと少なくとも残余ネットワークの増加パスが１長くなるので、繰り返し回数は高々 O(|V|)回となる。
よって計算量は O(|V|^2|E|).
Algorithm Dinic (G=(V,E),s,t)
1: 　for ( (u,v) \in E) {
2: 　　　　 f(u,v):=0; f(v,u):=0;
3: 　}
4: 　while (s-t path exists in Dinic's layered netrowk) {
5: 　　　　f:= blocking flow;
6: 　　　　augment flow by f;
7:　}

Dinic { /** O(|V|^2|E|) */
	@Override public Result solve(List<List<Edge>> adjList, int s, int t) {
		Result res = new Result(adjList);
		int n = adjList.size();
		boolean[] used = new boolean[n];
		for (boolean augmented = true; augmented; ) {
			augmented = false;
			calcLayreLevel(res, adjList, s, t); //make layered network
			Arrays.fill(used, false);
			while (true) {
				int f = augment(used, res, adjList, s, t, INF);
				if (f == 0) break;
				res.maximumFlow += f; augmented = true;
			}
		}
		return res;
	}
	private void calcLayreLevel(Result res, final List<List<Edge>> adjList, int s, int t) {
		Arrays.fill(res.trace, -1); res.trace[s] = 0; //trace[v] indicates level of v.
		Queue<Integer> q = new LinkedList<Integer>(); q.add(s);
		for (int lm = adjList.size(); !q.isEmpty() && res.trace[q.peek()] < lm; ) { //BFS
			int u = q.poll();
			if (u == t) lm = res.trace[u];
			for (Edge e : adjList.get(u)) if (res.trace[e.d] == -1 && res.residualCapacity(u, e.d) > 0) {
				res.trace[e.d] = res.trace[u] + 1;
				q.add(e.d);
			}
		}
	}
	private int augment(boolean[] used, Result res, final List<List<Edge>> adjList, int u, int t, int minC) { //DFS
		if (u == t) return minC;
		if (minC == 0 || used[u]) return 0;
		used[u] = true;
		for(Edge e : adjList.get(u)) if (res.trace[e.d] > res.trace[u]) { //level(e.d) > level(u)
			int f = augment(used, res, adjList, e.d, t, Math.min(minC, res.residualCapacity(u, e.d)));
			if (f > 0) {
				res.flow[u][e.d] += f; res.flow[e.d][u] -= f;
				used[u] = false;
				return f;
			}
		}
		return 0;
	}
}

Network Flow Algorithm

Algorithm

Network Flow Algorithms

フローネットワーク(Flow network)/輸送網(Transportation network)を扱うアルゴリズム。
各アークに容量(capacity)を設定し、各アークをフロー(flow)が流れる。
ネットワークフローアルゴリズムの適用分やには次のような物がある。
線形計画法(linear programming)に落とし込んでシンプレックスアルゴリズムを用いて解を求めることも可能だが、問題の変形と得られた解をもとの問題に適した形に戻す必要がある。また他のアルゴリズムで解いた方が速い場合がある。

  • 最小費用流問題(maximum cost flow problem)

供給節点sが複数ユニットを配布節点wのネットワークに流す。
これらは、需要節点tで消費される。各辺には、容量(low, high)、実際のフロー、この辺を流すときの１ユニットあたりのコストが付随する。
目標：需要のすべてを満たしながら、全辺での総コストを最小化する

  • 最大流問題(maximum flow problem)

最小費用流問題を特殊化。
ソース節点sが複数ユニットを配布節点w経由でシンク節点に到達するように流す。各辺には、容量と実際のフローが付随する。
目標：ネットワークフローFを最大にする
○Ford-Fulkerson algorithm O(|E|F_{\max})
○Edmonds-Karp algorithm O(|V||E|^2)
○Dinic's(Dinitz') algorithm O(|V|^2|E|)
○Goldberg-Tarjan(PUSH/RELABEL) algorithm O(|V||E|\log (|V|^2/|E|))※
　※様々な最適化/ヒューリスティックを加えた改良バージョンが存在する。並列化可能。

  • マッチング問題(matching problem)

Flow Network

  • N = (G, c, s, t):　フローネットワーク
  • G:　有向グラフ(通常、連結グラフ)
  • V:　Gの点集合
  • E(G)=\{ e=(u,v)|u,v\in V\} :　Gの辺集合
  • c(e):　辺eを流れることができるユニットの最大数を制限する容量(capacity)
  • e \in V:　シンク(sink)/目標(target)/終点(terminus)/流入点/出口. フローユニットを消費する特別なノード.
  • s \in V:　ソース(source)/湧出点/入口. フローユニットを生産する特別なノード.
  • f:E(G)\leftarrow \mathbb{R}^+:　辺を流れるユニット数を定義するフロー(flow)

※形式的に f:V\times V\rightarrow \mathbb{R}とする場合がある。

  • \delta^- (v):　vを終点とする辺集合
  • \delta^+ (v):　vを始点とする辺集合

fは次のような制約を満たさなければならない。

容量制約(Capacity constraints)

辺を流れるフローf(u,v)は、非負で、容量 c(u,v)を超えない。
\forall (u,v)\in E(G), 0\leq f(u,v)\leq c(u,v)　　※ (u,v)\not\in E(G)\Rightarrow c(u,v)=0

歪対称性(Skew symmetry)/反対称性(Asymmetry)

形式的に f:V\times V\rightarrow \mathbb{R}
f(v,u)=-f(u,v)とすれば、
これにより、ネットワークフローアルゴリズムがuからvへの正味のフローを決定する場合に、フローを足し合わせることができるようになる。

流量保存則(Flow conservation law)

ソースsとシンクtを除いた任意の接点に流入するフローの総和と流出するフローの総和は等しい。
ネットワークにおいて、sとtを除いては、フローの生産や消費が行われないという性質を保証する。
※Kirchhoffの電流則(KCL:Kirchhoff's Current Law)みたいなもんです。

  • \partial f(v) = \sum_{e\in\delta^+(v)}f(e) - \sum_{e\in\delta^-(v)}f(e):　vにおける流出量 - 流入量
  • \partial f:V\rightarrow \mathbb{R}:　フローの境界(boundary).

\forall v(\neq s, t)\in V, \partial f(v) = =0
歪対称性を考慮すれば、
\sum_v f(u,v) = 0, u\in V-\{s, t\} と書ける。

  • F = \partial f(s) = \sum_{e=(s,w)\in\delta^+(s)}f(e)-\sum_{e=(u,s)\in\delta^-(s)}f(e) = \sum_{e=(u,t)\in\delta^-(t)}f(e)-\sum_{e=(t,w)\in\delta^+(t)}f(e):　フローfの流量.

※通常 \sum_{e=(u,s)\in\delta^-(s)}f(e) = \sum_{e=(t,w)\in\delta^+(t)}f(e) = 0なので
F = \partial f(s) = \sum_{e=(s,w)\in\delta^+(s)}f(e) = \sum_{e=(u,t)\in\delta^-(t)}f(e)

  • F_{\max} = \max\{ F \}:　最大流
  • ネットワーク経路(network path)

閉路でない異なる節点列[tex: ]とEに含まれるn-1個の連続した辺 (v_i, v_j)からなる経路。ネットワーク経路では、辺の方向は無視できる。

残余ネットワーク(residual network)

  • c_f (e) = c(e)-f(e):　残余容量(residual capacity)
  • N(f) = (G(f), c_f, s, t):　残余ネットワーク(residual network)

利用可能な容量で構成されたネットワーク
本来のネットワークにはuからvへの辺がない場合でも、残余ネットワークではuからvへの辺がある場合もある。
反対向きのフローは相殺されるため、vからuへのフローが減少するということはuからvへのフローが増加することを意味する。
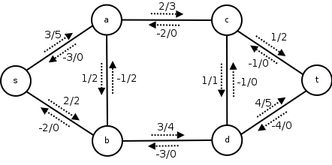
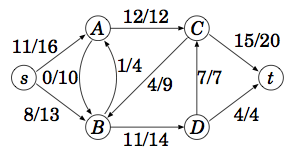
Network_flow Network_flow_2
フローネットワーク
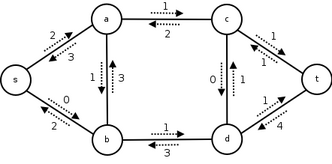
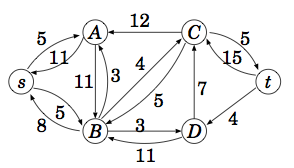
Network_flow_residual Network_flow_2_residual
残余ネットワーク

  • e^R=(w,v):　e=(v,w)の逆辺

※容量制約と歪対称性より c_f(e^R) = f(e)

  • E^R(G)=\{ e^R\in E\} :　仮想的な辺の集合
  • E(G(f))=\{ e\in E(G)| f(e)\leq c(e)\} \cup \{ e^R \in E^R(G) | f(e) > 0\}:　残余ネットワークにおける辺集合
  • P:　増加パス/道/経路(augmenting path)

u_1 = s, u_k = t, c_f(u_i, u_{i+1})>0となる残余ネットワーク上での単純経路(simple path，同じ頂点を2度以上通らない経路) (u_1, u_2, \cdots ,u_k).

  • c_P = \min\{ c_f(e)|(u,v)\in P \}:　増加パスPの容量. Pを通して c_Pだけ流量を増やすことができる。
  • 臨界辺(critical edge):　 e \in P, c_f(e) = c_P\ を満たす辺e
  • \delta_f (u,v):　N(f)上の頂点uからvへの最短距離(ホッポ数)

切断/カット(cut)

s\in S, t\in V-S=T, S\cap T = \emptyset
このときの(S, T)またはSをNのカットという.
従って、(S, T)の選び方は、 e^{|V|-2}種類ある。

  • E(S,T) = \{ (v,w)\in E(G)|v\in S, w\in T\} :　s-tカット
  • c(S, T) = \sum_{e\in E(S,T)}c(e):　(s-t)カットの容量
  • C_{\min} = \min \{ c(S, T) \}:　最小カット(容量)
  • f(S,T) = \sum_{e\in E(S,T)}f(e): SからTへの流量

最大流最小カット定理(max-flow min-cut theorem)

最大フロー F_{\max}=最小カット(容量) C_{\min}
※最大流問題を線形計画問題に落とし込むと、最小カット問題は双対問題(Dual Probrem)となっており、強双対定理(strong duality theorem)より、最大流最小カット定理が成り立つ。
※強双対定理：(P)または(D)のいずれか一方が最適解を持てば、もう一方も最適解を持ち、(P)の最適値と(D)の最適値は一致する。

  • Nの流量が最大 F= F_{\max} \cdots (I)
  • \equiv残余ネットワークN(f)は増加パスPを持たなない \cdots (II)
  • \equivNのあるカット(S,T)について F = c(S,T)\cdots (III)

証明

  • (I)→(II)

F = F_{\max}とし、N(f)は増加パスPをもつとすると、
N(f)のP上に流量F'>0が存在し、 F+F' > F_{\max }となり F_{\max}より大きい流量が得られることになり矛盾する。
従って、(I)→(II)

  • (II)→(III)

N(f)は増加パスPを持たないとすると、N(f)にsからtへのパスは存在しない。
S = {s, N(f)上でsから到達可能な頂点}とし、T = V - Sとすると、tはSに含まれないので、(S,T)はNのカットである。
S\times Tの任意の要素(u,v)において、 f(u,v) < c(u,v)であればvはSに含まれ矛盾するので、 f(u,v) = c(u,v).
ここで、f(T,S) \neq 0と仮定すると、NにTからSへ流れる辺が存在することになる。
するとSからTへの辺がN(f)に存在することになるが、これはN(f)にsからtへのパスは存在しないことと矛盾する。
従って、 f(T,S)=0
\therefore F = f(S,T)-f(T,S) = f(S,T) = \sum_{u\in S, v\in T}f(u,v) = \sum_{u\in S, v\in T}c(u,v) = c(S,T)（(II)→(III)）

  • (III)→(I)

F = C(S,T)となるカット(S,T)が存在するとする。
F = f(S,T)-f(T,S)
フローは非負なので、
0\leq f(T,S)\leq f(S,T)
F\leq f(S,T)-f(T,S)+f(T,S)
\therefore F\leq f(S,T)
フローネットワークの容量制約のため、辺に容量を超えたフローを流すことはできないので、
F\leq f(S,T)\leq c(S,T)
\therefore F\leq c(S,T)\cdots (*)
ここで、(*)は、
Fがc(S,T)の下界、c(S,T)がFの上界であるとことを示している。
従って、F=c(S,T)が存在するなら、そのとき、
F_{\max}=C_{\min}となる。（(III)→(II)）

Dinitz(Dinic)の層別ネットワーク(layered network)/レベルネットワーク(level network)

  • level(v):　各点vのsからの距離(辺数最小の増加パスに含まれる辺数)
  • V_k = \{ v| {\rm level}(v)=k, v\in V\} :　層(layer). V_0 = \{s \}とする.
  • E_L (f) = \{ (u, v) \in E(G(f)) | {\rm level}(v) = {\rm level}(u)+1 \} :　 V_k, V_{k+1}を結ぶ辺集合
  • V_L (f)=\{ v | v\in V_0, V_1,\cdots \}:　 V_0, V_1, \cdots をあわせた点集合
  • G_L = (V_L, E_L):　層別ネットワークのグラフ要素
  • N_L (f) = (G_L, c_f, s, t): Dinitz(Dinic)'s layered network/level network.
  • f''(e):　 N_L (f)でのeのフロー.
  • ブロッキングフロー(blocking flow):　各s-tパスにいくつかのsaturated arc(流量=容量となっている辺)を含むようなフロー

Dinic2Dinic
ネットワークフロー
Dinic2_residualDinic_residual
残余ネットワーク
Dinic2_layeredDinic_layered
層別ネットワーク

Cats Going Straight II(AOJ No.0273)

Online judge

リポジトリ

Cats Going Straight II(AOJ No.0273)

まっすぐな壁で囲まれたいくつかの部屋からなるお屋敷がある。
お屋敷の一番外側の壁をみると、凸多角形になっている。
１枚の壁はその両端にある柱によって支えられている。

  • 異なる柱が同じ位置を占めることはない。
  • 異なる壁が重なったり、柱以外で交差することはない。
  • １つの柱は２つ以上の壁を支えている。
  • 壁の長さは 0 より大きい。
  • 柱は壁の両端だけにある。つまり、柱が壁の途中にあることはない。
  • 壁は異なる２つの部屋、あるいは部屋と外とを仕切る。
  • 任意の異なる２つの柱を選んだとき、互いの柱には壁をたどって到達できる。

お屋敷の部屋のどこかに猫がおり、猫は壁をすり抜けることができる。
猫が「最良の選択」をした場合、外に出るまでに通る穴の数の最大値を求める。
制約
-1000 ≤ 座標 ≤ 1000
3 ≤ 柱の数、壁の数 ≤ 100

アルゴリズム

双対グラフを作って、BFSで外に相当するノードから各部屋に相当するノードへの距離(ホップ数)を求める。

双対グラフを作るにはまず、領域を求めなければならない。
双方向の有向グラフを考え、各辺を半時計回りにソートした隣接リストで元のグラフを表現する。
半時計回りにソートするには、始点から終点への方向ベクトルの偏角 [ -\pi, \pi] の昇順にソートすれば良い。
そして、有向辺に属す領域を示す色を塗っていく。
色が塗られていない有向辺に色を割り当てて、その逆辺から半時計回りにある辺に同じ色を塗る。これを繰り返してもとの有向辺にもどってきたら一つ領域分の色が塗り終わる。これを全てのアークに色がつくまで行うとすべての領域が求まる。
最後にある有向辺とその逆辺の領域(色)を結ぶと双対グラフができる。
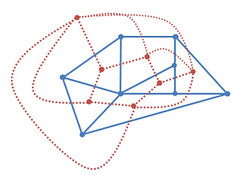
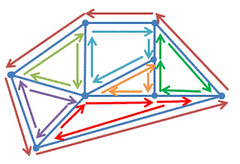
dualgraphcoloringRegion
元の(彩色済みの有向)グラフでは、一番左のノードからでる有向辺のうち一番偏角が小さい（ -\piに近い）有向辺が外に対応する色が塗られている。
それに対応する双対グラフのノードからDFSを行う。ホップ数の最大値が答え。

コード

Edgeの情報として、終点ノードのインデックス、始点から終点への方向ベクトルの偏角、(ソート済みのリストでの)逆辺のインデックス、色（領域）を持たせた。
偏角はMath.atan2を使って求める。

import java.util.*;
import java.awt.Point;
public class aoj0273 {
	static final Scanner stdin = new Scanner(System.in);
	static Point[] points;
	public static void main(String[] args) {
		while (true) {
			int n = stdin.nextInt(), W = stdin.nextInt();
			if ((n|W) == 0) break;
			points = new Point[n];
			for (int i = 0; i < n; ++i) points[i] = new Point(stdin.nextInt(), stdin.nextInt());
			List<List<Edge>> adjList = new ArrayList<List<Edge>>(n);
			for (int i = 0; i < n; ++i) adjList.add(new ArrayList<Edge>());
			while (W-- > 0) {
				int src = stdin.nextInt()-1, dst = stdin.nextInt()-1;
				adjList.get(src).add(new Edge(src, dst)); adjList.get(dst).add(new Edge(dst, src));
			}
			boolean[][] adjMatrix = buildDualGraph(adjList, n);
			int mi = 0, mx = points[mi].x;
			for (int i = 1; i < n; ++i) if (mx > points[i].x) { mi = i; mx = points[i].x; }
			int out = adjList.get(mi).get(0).region;
			
			n = adjMatrix.length;
			int[] dist = new int[n];
			Arrays.fill(dist, -1);
			Queue<Integer> q = new LinkedList<Integer>();
			q.add(out);
			dist[out] = 0;
			while (!q.isEmpty()) {
				int p = q.poll();
				for (int r = 0; r < n; ++r) if (adjMatrix[p][r] && dist[r] == -1) {
					dist[r] = dist[p] + 1;
					q.add(r);
				}
			}
			int ans = -1;
			for (int d : dist) ans = Math.max(ans, d);
			System.out.println(ans);
		}
	}
	static boolean[][] buildDualGraph(List<List<Edge>> adjList, int n) {
		for (List<Edge> l : adjList) Collections.sort(l);
		for (int i = 0; i < n; ++i) for (Edge e : adjList.get(i)) {
			int idx = -1;
			while (adjList.get(e.dst).get(++idx).dst != i);
			e.rev = idx;
		}
		int regionID = 0;
		for (int i = 0; i < n; ++i) for (int j = 0; j < adjList.get(i).size(); ++j) 
			if (adjList.get(i).get(j).region == -1) setRegion(adjList, i, j, regionID++);
		boolean[][] adjMatrix = new boolean[regionID][regionID];
		for (List<Edge> l : adjList) for (int j = 0, k = l.size()-1; j < l.size(); k = j++) {
			int src = l.get(k).region, dst = l.get(j).region;
			adjMatrix[src][dst] = adjMatrix[dst][src] = true;
		}
		return adjMatrix;
	}
	static void setRegion(List<List<Edge>> adjList, int i, int j, int regionID) {
		while (true) {
			Edge e = adjList.get(i).get(j);
			int ni = e.dst, nj = (e.rev + 1) % adjList.get(ni).size();
			Edge ne = adjList.get(ni).get(nj);
			if (ne.region != -1) break;
			ne.region = regionID;
			i = ni; j = nj;
		}
	}
	static class Edge implements Comparable<Edge> {
		int region = -1, dst, rev;
		double arg;
		Edge(int src, int dst) { 
			this.dst = dst;
			this.arg = Math.atan2(points[dst].y - points[src].y, points[dst].x - points[src].x);
		}
		@Override public int compareTo(Edge o) { return Double.compare(this.arg, o.arg); }
	}
}

平面グラフ(plane graph)、彩色(cloring)、木(tree)

Math

平面グラフ(plane graph)

辺が交差しないように平面上に描けるグラフ(多重グラフを含む)は、平面的(planer)であるといい、特に、有限多重グラフの平面表現は地図(map)(または単に平面グラフ(plane graph))と呼ばれる。平面グラフと同型なグラフのことを平面的グラフ (planar graph) という。

  • 領域(region)の次数(degree):領域rの境界の閉路または閉じた歩道の長さを領域rの次数(degree)という。

planeGraph
\deg (r_1)=3, \deg (r_2)=3, \deg (r_3)=5, \deg (r_4) = 4, \deg (r_5)=3
※ r_3の境界である閉じた歩道は (C,D,E,F,E,C)


各辺は、２つの領域の境界であるか、領域にふくまれるかのいずれかであり、
後者は、領域の境界に沿ったどんな閉じた歩道においても２度現れるため、（頂点の次数と同様に、）
\sum_r \deg(r) = 2|E|\cdots (1)
が成り立つ。

Eulerの公式(Euler's formula)

連結平面グラフG(V,E)の領域の個数をRとしたとき、
|V| - |E| + R = 2 \cdots (2)
(証明)
頂点が一つだけのグラフの場合、 |V|=1, |E|=0, R=1なので(2)を満たす。
他の場合の連結平面グラフは、頂点が１つだけのグラフに、次の(I)または(II)の操作をすることで構成される。

  • (I):新しい頂点v2を加え、それまでの辺と交差しないように、v2ともとからある頂点v1を結ぶ辺を加える
  • (II):それまでの辺と交差しないように、もとからある頂点v1,v2間を結ぶ辺を加える

(I)の操作では、|V|と|E|の値がどちらも１増えるので、操作後も|V|-|E|+Rの値は変わらない。
(II)の操作では、|E|とRの値がどちらも１増えるので、操作後も|V|-|E|+Rの値は変わらない。
したがって、１個の頂点だけのグラフのときと同じ|V|-|E|+Rの値を持たなければならない。
以上より、(2)が成り立つ。（証明終わり）

  • 連結平面的グラフG(V,E), |V| = p \geq 3, |E| = q を考えたとき、

q \leq 3p-6 \cdots (3)
(証明)
Gの平面的表現における領域の数とすると、Eulerの公式(2)より、
p-q+r = 2\cdots (a)
また、(1)より、領域の次数の和は2qに等しい。各領域の次数は３以上なので、
2q\geq 3r
これを(a)に代入すると、
2 = p-q+r \leq p - q + \frac{2q}{3}
すなわち 2\leq p - \frac{q}{3}
両辺に3をかけて、(3)が得られる。(証明終わり)

Kuratowskiの定理(Kuratowski's theorem)

グラフが非平面的であるのは、 K_{3,3}または K_5と同窓な部分グラフを含むときかつそのときに限る。 \cdots (4)
Kuratowski's theorem - Wikipedia, the free encyclopedia
※ K_{3,3}は各頂点の次数が3の２部グラフ(設備グラフ(utility graph)).
※ K_5は頂点が５つの完全正則グラフ.

  • 彩色(coloring)　隣接した頂点が異なる色を持つようにGの拡張点へ色を割り当てることを頂点彩色(vertex coloring)または、彩色(coloring)という。n色が使われるGの彩色が存在するとき、n-彩色可能(n-colorable)であるという。

染色数(chromatic number)：グラフGを塗るのにひつような色の最小数をGの染色数といい、 \chi (G)と書く。

Welsh–Powellアルゴリズム(Welsh–Powell algorithm)

Gを彩色するアルゴリズム
※このアルゴリズムで染色数は決定できない(塗る色の数が最小になるとは限らない)
※離散数学―コンピュータサイエンスの基礎数学 (マグロウヒル大学演習)ではWelchという表記になってますが、ググったところwelshの方が多数派ぽいのでwelshにしときました。

//グラフGの頂点をv[i](i = 0, 2, ..., n-1)とする
Step1.　deg(v[i])を求める。(i = 0, 2, ..., n-1)
Step2.　deg(v[i])の降順に頂点vをソートする。
Step3.　以下の操作を全ての頂点が彩色されるまで繰り返す。
Step3-1.　新しい色にCを更新し、無色で一番次数が高い頂点v[k]に色Cを塗る。
Step3-2.　v[k]と隣接していない無色の頂点すべてに色Cを塗る。

Boost.GraphでWelsh–Powellアルゴリズムを実装している方がいたのでリンク貼っときます。
グラフ理論 Welsh-Powellの頂点彩色アルゴリズムを実装してみた - devm33の備忘録
Welsh-Powellで彩色数にならない例 - devm33の備忘録

  • グラフGについて

Gは2-彩色可能
\equivGは2部グラフ
\equivGの各閉路が偶数の長さを持つ \cdots (5)

  • 双対グラフ(dual graph):　地図すなわち有限多重平面的グラフGの、各領域の中に１つ頂点をとり、２つの領域が共通の辺を持つとき、その共通な辺と交差する曲線で対応する頂点を結ぶ辺を加えたとき、その辺を互いに交わらないように書くことができる。このようにしてできたグラフG*は双対(dual)であるといい、G*をGの双対グラフ(dual graph)という。また、GはG*の双対グラフになっている。

dualgraph
双対グラフの作り方の例(Cats Going Straight II(AOJ No.0273))

４色定理(four color theorem)

全ての平面的グラフは(頂点)4-彩色可能である \cdots (6)
※プログラムによる網羅的証明 Four color theorem - Wikipedia, the free encyclopedia

  • 森(forest):　閉路を持たない、無閉路的(acyclic)、非閉路的(cycle-free)なグラフ。(森の連結成分は木)。
  • 木(tree):　連結な森。
  • 退化木(degenerate tree):　１個の頂点で構成され、辺を持たない木。
  • Gを2個以上の頂点を持つグラフとするとき、

Gは木である。
\equivGの頂点の全ての対は、ちょうど１個の道で結ばれている。
\equivGは連結であるが、どの辺を除いても非連結なグラフになる。
\equivGは非閉路的であるが、どのように辺を加えても、ちょうど１個の閉路をもつグラフになる。 \cdots (7)

  • Gをn>1個の頂点を持つ有限グラフとするとき、

Gは木である。
\equivGは非閉路的であり、n-1本の辺を持つ。
\equivGは連結であり、n-1本の辺を持つ。 \cdots (8)

  • Gが木(または森)

\RightarrowGは2-彩色可能である。
\RightarrowGは２部グラフである。 \cdots (9)
逆は真ではない。

全域木(spanning tree):

TがGの部分グラフで、Gの全ての頂点を含んだ木であるとき、Tを全域木という。とくに、辺の長さの総和が最小になる全域木を最小全域木(minimum spanning tree)という。

根付き木(rooted tree):

指定された木の根(root)を持つ木。

  • 水準(level)、深さ(depth):　根rから頂点vまでの道の長さは、vの水準(level)または、vの深さ(depth)とよばれる。
  • 葉(leaf):　r以外の次数1の頂点
  • 枝(branch):　頂点から葉までの道
  • 範囲(scope):　頂点vを根とし、vに後続する頂点全てを含む部分木

根rからuを含むvへの道があるとき、uはvに先行する(preceedes)、あるいは、vはuに後続する(fllows)という。
特に、vがuに後続していて、uに隣接しているなら、vはuの直後(immediately follows)であるという。

  • 順序根付き木(ordered rooted tree):　拡張点から出る辺が順序つけられている根付き木。

The Lonely Girl's Lie(AOJ No.0272)

Online judge

リポジトリ

The Lonely Girl's Lie(AOJ No.0272)

N
a1 a2 ... aN
b1 b2 ... bN
が与えられる。
aiはAがもっているパケモンのレベルbiはBがもっているパケモンのレベルを示す。
パケモンを戦わせたとき、レベルが高い方が勝つ。同レベルなら引き分け。
お互いk匹パケモンを選んで１対１でk回戦したとき、Aの勝ち数が必ずk/2より大きくなるようなkの最小値を求める。
どう選んでも勝てない場合はNAと答える。
制約
1 ≤ N ≤ 40000
1 ≤ ai,bi ≤ 100000
1 ≤ k < N

アルゴリズム

お互いの最前手は強い順でk匹選んだ場合。
強い順にソートし、
kを増やしながら2分探索して
Aの勝ち数 = k - Bの勝ちor引き分け数
を求める。
境界条件を間違えないようにする。
k == NはNA

コード

Collections.reverseOrder()便利。プリミティブ型には使えないけど。
Memory Limit Exceededたくさん出した。
毎回配列を生成したり、コンパレータを渡しているのがまずいのかと思って直して提出してみたけど、
やっぱりMemory Limit Exceededじゃないか...（呆れ）
System.gc()を入れてとおりました。競技プログラミングでガーベジコレクションとか正気か？

import java.util.*;
public class aoj0272 {
    static final Scanner stdin = new Scanner(System.in);
    public static void main(String[] args) {
        while (true) {
            int n = stdin.nextInt();
            if (n == 0) break;
            System.gc();
            Integer[] a = new Integer[n], b = new Integer[n];
            for (int i = 0; i < n; ++i) a[i] = stdin.nextInt();
            for (int i = 0; i < n; ++i) b[i] = stdin.nextInt();
            Arrays.sort(a, Collections.reverseOrder());
            Arrays.sort(b, Collections.reverseOrder());
            int k = n;
            for (int i = 0, bNotFail = 0; i < n; ++i) {
                k = i+1;
                int pos = lowerBound(b, a[i]-1, Collections.reverseOrder())-1;
                if (bNotFail <= pos) ++bNotFail;
                if ((k - bNotFail) > k/2) break;
            }
            System.out.println(k < n ? k : "NA");
        }
    }
    public static <T> int lowerBound(T[] a, int fromIndex, int toIndex, T key, Comparator<? super T> c){
        int lb = fromIndex - 1, ub = toIndex;
        while(ub - lb > 1){          //rage of solution > 1
            int mid = (lb + ub) / 2, cmp = c.compare(a[mid], key);
            if( cmp >= 0 )   ub = mid;   //(lb,mid]
            else            lb = mid;   //(mid,ub]
        }
        return ub;                      //(lb, ub], ub = lb + 1 → [ub, ub+1)
    }
    public static <T> int lowerBound(T[] a, T key, Comparator<? super T> c){
		return lowerBound(a, 0, a.length, key, c);
	}
}

Izua Dictionary(AOJ No.0271)

Online judge

リポジトリ

Izua Dictionary(AOJ No.0271)

nと、0, 1, ..., n-1を並べ替えてできるn!個の数列が辞書に乗っている。
数列0, 1, ..., n-1を入力に従ってR回スワップしてできた数列 x_0, x_1, \cdots x_{n-1}が辞書の何番目に乗っているかを答える。
ただし、0, 1, ..., n-1は、0番目に乗っていると数える。
答えは,大きな数になりうるので1,000,000,007の剰余で答える。
制約
1 ≤ n ≤ 100000 = N
0 ≤ R ≤ 50

アルゴリズム

先頭から１文字筒注目し、辞書順で何番目かを求め、総和を求める。
\sum_{i=0}^{n-1} (x_i - \sum_{j < i, x_j < x_i}1)(n-1-i)!　　 \pmod{1,000,000,007}
あんま上手く説明できないけど、
(n-1-i)!がi番目より後ろの並べ方。係数は0から x_iの中ですでに使用したものを除いたアルファベットの候補数。
(n-1-i)!は階乗のテーブルを始めに使っておき、
\sum_{j < i, x_j < x_i}1はbinary indexed treeを使用すれば低コストで計算できる。

コード

import java.util.*;
public class aoj0271 {
    static final Scanner stdin = new Scanner(System.in);
    static final int MOD = 1000000007, NMAX = 100001, seq[] = new int[NMAX], input[] = new int[NMAX];
    static final long factMod[] = new long[NMAX];
    static {
        factMod[0] = 1;
        for (int i = 1; i < NMAX; ++i) {
            factMod[i] = (factMod[i-1]*i) % MOD;
            seq[i] = i;
        }
    }
    public static void main(String[] args) {
        while (true) {
            int N = stdin.nextInt();
            if (N == 0) break;
            FenwickTree BIT = new FenwickTree(N+1);
            System.arraycopy(seq, 0, input, 0, N);
            int R = stdin.nextInt();
            while (R-- > 0) {
                int a = stdin.nextInt()-1, b = stdin.nextInt()-1;
                int tmp = input[a]; input[a] = input[b]; input[b] = tmp;
            }
            long ans = 0;
            for (int i = 0; i < N; i++) {
                int cnt = input[i] - BIT.sum(input[i]);
                ans = (ans + cnt * factMod[N-i-1]) % MOD;
                BIT.add(input[i], 1);
            }
            System.out.println(ans);
        }
    }
    public static class FenwickTree {
        private int[] x;
        public FenwickTree(int n){ init(n);}
        public final void init(int n){ x = new int[n]; Arrays.fill(x, 0); }
        public final int sum(int i){
            int ret = 0;
            for(int j = i; j >= 0; j = ((j & (j+1)) - 1)) ret += x[j];
            return ret;
        }
        public final void add(int i, int a){
            for(int j = i; j < x.length; j |= j+1) x[j] += a;
        }
    }
}