Network Flow Algorithm - kanetaiの二次記憶装置

Network Flow Algorithms

フローネットワーク(Flow network)/輸送網(Transportation network)を扱うアルゴリズム。
各アークに容量(capacity)を設定し、各アークをフロー(flow)が流れる。
ネットワークフローアルゴリズムの適用分やには次のような物がある。
線形計画法(linear programming)に落とし込んでシンプレックスアルゴリズムを用いて解を求めることも可能だが、問題の変形と得られた解をもとの問題に適した形に戻す必要がある。また他のアルゴリズムで解いた方が速い場合がある。

最小費用流問題(maximum cost flow problem)

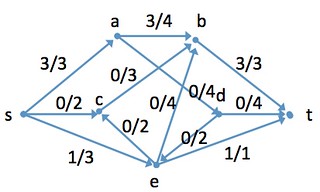
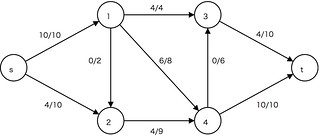
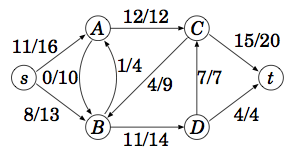
供給節点sが複数ユニットを配布節点wのネットワークに流す。
これらは、需要節点tで消費される。各辺には、容量(low, high)、実際のフロー、この辺を流すときの１ユニットあたりのコストが付随する。
目標：需要のすべてを満たしながら、全辺での総コストを最小化する

最大流問題(maximum flow problem)

最小費用流問題を特殊化。
ソース節点sが複数ユニットを配布節点w経由でシンク節点に到達するように流す。各辺には、容量と実際のフローが付随する。
目標：ネットワークフローFを最大にする
○Ford-Fulkerson algorithm $O(|E|F_{\max})$
○Edmonds-Karp algorithm $O(|V||E|^2)$
○Dinic's(Dinitz') algorithm $O(|V|^2|E|)$
○Goldberg-Tarjan(PUSH/RELABEL) algorithm $O(|V||E|\log (|V|^2/|E|))$ ※
　※様々な最適化/ヒューリスティックを加えた改良バージョンが存在する。並列化可能。

マッチング問題(matching problem)

Flow Network

N = (G, c, s, t):　フローネットワーク
G:　有向グラフ(通常、連結グラフ)
V:　Gの点集合
$E(G)=\{ e=(u,v)|u,v\in V\}$ :　Gの辺集合
c(e):　辺eを流れることができるユニットの最大数を制限する容量(capacity)
$e \in V$ :　シンク(sink)/目標(target)/終点(terminus)/流入点/出口. フローユニットを消費する特別なノード.
$s \in V$ :　ソース(source)/湧出点/入口. フローユニットを生産する特別なノード.
$f:E(G)\leftarrow \mathbb{R}^+$ :　辺を流れるユニット数を定義するフロー(flow)

※形式的に $f:V\times V\rightarrow \mathbb{R}$ とする場合がある。

$\delta^- (v)$ :　vを終点とする辺集合
$\delta^+ (v)$ :　vを始点とする辺集合

fは次のような制約を満たさなければならない。

容量制約(Capacity constraints)

辺を流れるフローf(u,v)は、非負で、容量 $c(u,v)$ を超えない。
$\forall (u,v)\in E(G), 0\leq f(u,v)\leq c(u,v)$ 　　※ $(u,v)\not\in E(G)\Rightarrow c(u,v)=0$

歪対称性(Skew symmetry)/反対称性(Asymmetry)

形式的に $f:V\times V\rightarrow \mathbb{R}$
$f(v,u)=-f(u,v)$ とすれば、
これにより、ネットワークフローアルゴリズムがuからvへの正味のフローを決定する場合に、フローを足し合わせることができるようになる。

流量保存則(Flow conservation law)

ソースsとシンクtを除いた任意の接点に流入するフローの総和と流出するフローの総和は等しい。
ネットワークにおいて、sとtを除いては、フローの生産や消費が行われないという性質を保証する。
※Kirchhoffの電流則(KCL:Kirchhoff's Current Law)みたいなもんです。

$\partial f(v) = \sum_{e\in\delta^+(v)}f(e) - \sum_{e\in\delta^-(v)}f(e)$ :　vにおける流出量 - 流入量
$\partial f:V\rightarrow \mathbb{R}$ :　フローの境界(boundary).

$\forall v(\neq s, t)\in V, \partial f(v) = =0$
歪対称性を考慮すれば、
$\sum_v f(u,v) = 0, u\in V-\{s, t\}$ と書ける。

$F = \partial f(s) = \sum_{e=(s,w)\in\delta^+(s)}f(e)-\sum_{e=(u,s)\in\delta^-(s)}f(e) = \sum_{e=(u,t)\in\delta^-(t)}f(e)-\sum_{e=(t,w)\in\delta^+(t)}f(e)$ :　フローfの流量.

※通常 $\sum_{e=(u,s)\in\delta^-(s)}f(e) = \sum_{e=(t,w)\in\delta^+(t)}f(e) = 0$ なので
$F = \partial f(s) = \sum_{e=(s,w)\in\delta^+(s)}f(e) = \sum_{e=(u,t)\in\delta^-(t)}f(e)$

$F_{\max} = \max\{ F \}$ :　最大流

ネットワーク経路(network path)

閉路でない異なる節点列[tex: ]とEに含まれるn-1個の連続した辺 $(v_i, v_j)$ からなる経路。ネットワーク経路では、辺の方向は無視できる。

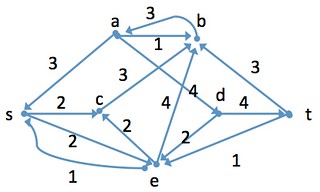
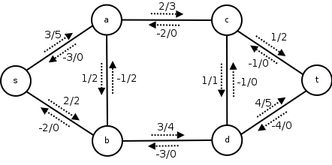
残余ネットワーク(residual network)

$c_f (e) = c(e)-f(e)$ :　残余容量(residual capacity)
$N(f) = (G(f), c_f, s, t)$ :　残余ネットワーク(residual network)

利用可能な容量で構成されたネットワーク
本来のネットワークにはuからvへの辺がない場合でも、残余ネットワークではuからvへの辺がある場合もある。
反対向きのフローは相殺されるため、vからuへのフローが減少するということはuからvへのフローが増加することを意味する。

フローネットワーク

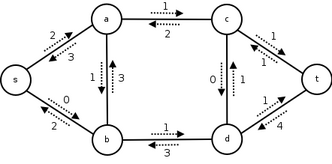
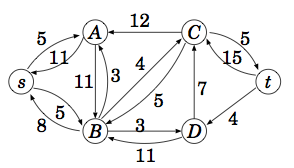
残余ネットワーク

$e^R=(w,v)$ :　e=(v,w)の逆辺

※容量制約と歪対称性より $c_f(e^R) = f(e)$

$E^R(G)=\{ e^R\in E\}$ :　仮想的な辺の集合
$E(G(f))=\{ e\in E(G)| f(e)\leq c(e)\} \cup \{ e^R \in E^R(G) | f(e) > 0\}$ :　残余ネットワークにおける辺集合

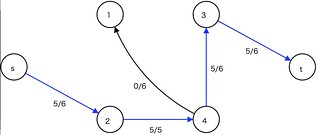
P:　増加パス/道/経路(augmenting path)

$u_1 = s, u_k = t, c_f(u_i, u_{i+1})>0$ となる残余ネットワーク上での単純経路(simple path，同じ頂点を2度以上通らない経路) $(u_1, u_2, \cdots ,u_k)$ .

$c_P = \min\{ c_f(e)|(u,v)\in P \}$ :　増加パスPの容量. Pを通して $c_P$ だけ流量を増やすことができる。
臨界辺(critical edge):　 $e \in P, c_f(e) = c_P\$ を満たす辺e
$\delta_f (u,v)$ :　N(f)上の頂点uからvへの最短距離(ホッポ数)

切断/カット(cut)

$s\in S, t\in V-S=T, S\cap T = \emptyset$
このときの(S, T)またはSをNのカットという.
従って、(S, T)の選び方は、 $e^{|V|-2}$ 種類ある。

$E(S,T) = \{ (v,w)\in E(G)|v\in S, w\in T\}$ :　s-tカット
$c(S, T) = \sum_{e\in E(S,T)}c(e)$ :　(s-t)カットの容量
$C_{\min} = \min \{ c(S, T) \}$ :　最小カット(容量)
$f(S,T) = \sum_{e\in E(S,T)}f(e)$ : SからTへの流量

最大流最小カット定理(max-flow min-cut theorem)

最大フロー $F_{\max}$ =最小カット(容量) $C_{\min}$
※最大流問題を線形計画問題に落とし込むと、最小カット問題は双対問題(Dual Probrem)となっており、強双対定理(strong duality theorem)より、最大流最小カット定理が成り立つ。
※強双対定理：(P)または(D)のいずれか一方が最適解を持てば、もう一方も最適解を持ち、(P)の最適値と(D)の最適値は一致する。

Nの流量が最大 $F= F_{\max} \cdots (I)$
$\equiv$ 残余ネットワーク $N(f)$ は増加パスPを持たなない $\cdots (II)$
$\equiv$ Nのあるカット(S,T)について $F = c(S,T)\cdots (III)$

証明

(I)→(II)

$F = F_{\max}$ とし、 $N(f)$ は増加パスPをもつとすると、
$N(f)$ のP上に流量F'>0が存在し、 $F+F' > F_{\max }$ となり $F_{\max}$ より大きい流量が得られることになり矛盾する。
従って、(I)→(II)

(II)→(III)

N(f)は増加パスPを持たないとすると、N(f)にsからtへのパスは存在しない。
S = {s, N(f)上でsから到達可能な頂点}とし、T = V - Sとすると、tはSに含まれないので、(S,T)はNのカットである。
$S\times T$ の任意の要素(u,v)において、 $f(u,v) < c(u,v)$ であればvはSに含まれ矛盾するので、 $f(u,v) = c(u,v)$ .
ここで、 $f(T,S) \neq 0$ と仮定すると、NにTからSへ流れる辺が存在することになる。
するとSからTへの辺がN(f)に存在することになるが、これはN(f)にsからtへのパスは存在しないことと矛盾する。
従って、 $f(T,S)=0$
$\therefore F = f(S,T)-f(T,S) = f(S,T) = \sum_{u\in S, v\in T}f(u,v) = \sum_{u\in S, v\in T}c(u,v) = c(S,T)$ （(II)→(III)）

(III)→(I)

$F = C(S,T)$ となるカット(S,T)が存在するとする。
$F = f(S,T)-f(T,S)$
フローは非負なので、
$0\leq f(T,S)\leq f(S,T)$
$F\leq f(S,T)-f(T,S)+f(T,S)$
$\therefore F\leq f(S,T)$
フローネットワークの容量制約のため、辺に容量を超えたフローを流すことはできないので、
$F\leq f(S,T)\leq c(S,T)$
$\therefore F\leq c(S,T)\cdots (*)$
ここで、(*)は、
Fがc(S,T)の下界、c(S,T)がFの上界であるとことを示している。
従って、F=c(S,T)が存在するなら、そのとき、
$F_{\max}=C_{\min}$ となる。（(III)→(II)）

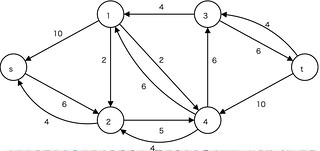
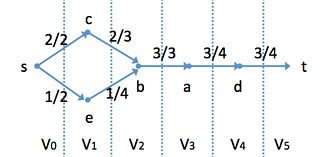
Dinitz(Dinic)の層別ネットワーク(layered network)/レベルネットワーク(level network)

level(v):　各点vのsからの距離(辺数最小の増加パスに含まれる辺数)
$V_k = \{ v| {\rm level}(v)=k, v\in V\}$ :　層(layer). $V_0 = \{s \}$ とする.
$E_L (f) = \{ (u, v) \in E(G(f)) | {\rm level}(v) = {\rm level}(u)+1 \}$ :　 $V_k, V_{k+1}$ を結ぶ辺集合
$V_L (f)=\{ v | v\in V_0, V_1,\cdots \}$ :　 $V_0, V_1, \cdots$ をあわせた点集合
$G_L = (V_L, E_L)$ :　層別ネットワークのグラフ要素
$N_L (f) = (G_L, c_f, s, t)$ : Dinitz(Dinic)'s layered network/level network.
$f''(e)$ :　 $N_L (f)$ でのeのフロー.
ブロッキングフロー(blocking flow):　各s-tパスにいくつかのsaturated arc(流量=容量となっている辺)を含むようなフロー

ネットワークフロー

残余ネットワーク

層別ネットワーク